四阶龙格库塔方法求解一次常微分方程组

一、写在前面

龙格库塔方法是数值求解常微分非线性方程的有利工具，计算精度较高，通过缩短步进距离和增加阶数可以进一步控制误差范围。工程上较为常用的是四阶龙格库塔算法（R-K4)，在计算收敛的情况下往往可以得到比较好的结果。

二、四阶龙格库塔方法

这里简单介绍一下算法的具体实现过程，不做详细的推导。其求解的问题是形如方程：

$$\dot{y}=f(y,t), and t\in[t_0,t_1] \\ init y(t_0)=c_0$$

通过选取一定的步进长度h，来对区间上函数值进行单步迭代求解，最终得到结果。具体计算公式为：

$$t_{n+1}=t_n+h\\ k_1=f(y_n,t_n)\\ k_2=f(y_n+\dfrac{h}{2}k_1,t_n+\dfrac{h}{2})\\ k_3=f(y_n+\dfrac{h}{2}k_2,t_n+\dfrac{h}{2})\\ k_4=f(y_n+hk_3,t_n+h)\\ y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)$$

通过以上公式，选取合适的步进长度h，反复迭代，就可求解出y的数值解。

三、使用四阶龙格库塔方法求解一次常微分方程组

• 使用的环境matlabR2019a
• 求解的方程

$$\dot{x}=y+3z+sin(5t)\\ \dot{y}=x+cos(t)\\ \dot{z}=x+z-3cos(3t)sin(4t)\\ and t\in[0,1]\\ x(0)=y(0)=z(0)=1$$

• matlab代码

clear;
clc;
close all;

h=1e-5;      %步进长度
t=0:h:1;   %生成自变量t的向量

%%创建计算结果x，y，z的数组
N=length(t);
x=ones(1,N);
y=ones(1,N);
z=ones(1,N);

%%四阶龙格库塔迭代
for i=2:N
    t_n=t(i-1);
    x_n=x(i-1);
    y_n=y(i-1);
    z_n=z(i-1);
    
    kx1=y_n+3*z_n+sin(5*t_n);
    ky1=x_n+cos(t_n);
    kz1=x_n+z_n-3*cos(3*t_n)*sin(4*t_n);
    
    kx2=(y_n+ky1*h/2)+3*(z_n+kz1*h/2)+sin(5*(t_n+h/2));
    ky2=(x_n+kx1*h/2)+cos(t_n+h/2);
    kz2=(x_n+kx1*h/2)+(z_n+kz1*h/2)-3*cos(3*(t_n+h/2))*sin(4*(t_n+h/2));
    
    kx3=(y_n+ky2*h/2)+3*(z_n+kz2*h/2)+sin(5*(t_n+h/2));
    ky3=(x_n+kx2*h/2)+cos(t_n+h/2);
    kz3=(x_n+kx2*h/2)+(z_n+kz2*h/2)-3*cos(3*(t_n+h/2))*sin(4*(t_n+h/2));
    
    kx4=(y_n+ky3*h)+3*(z_n+kz3*h)+sin(5*(t_n+h));
    ky4=(x_n+kx3*h)+cos(t_n+h);
    kz4=(x_n+kx3*h)+(z_n+kz3*h)-3*cos(3*(t_n+h))*sin(4*(t_n+h));
    
    x(i)=x_n+h/6*(kx1+2*kx2+2*kx3+kx4);
    y(i)=y_n+h/6*(ky1+2*ky2+2*ky3+ky4);
    z(i)=z_n+h/6*(kz1+2*kz2+2*kz3+kz4);  
end
%%画图
figure();
hold on;
plot(t,x,'r');
plot(t,y,'g');
plot(t,z,'b');
legend('x','y','z');
xlabel('t');
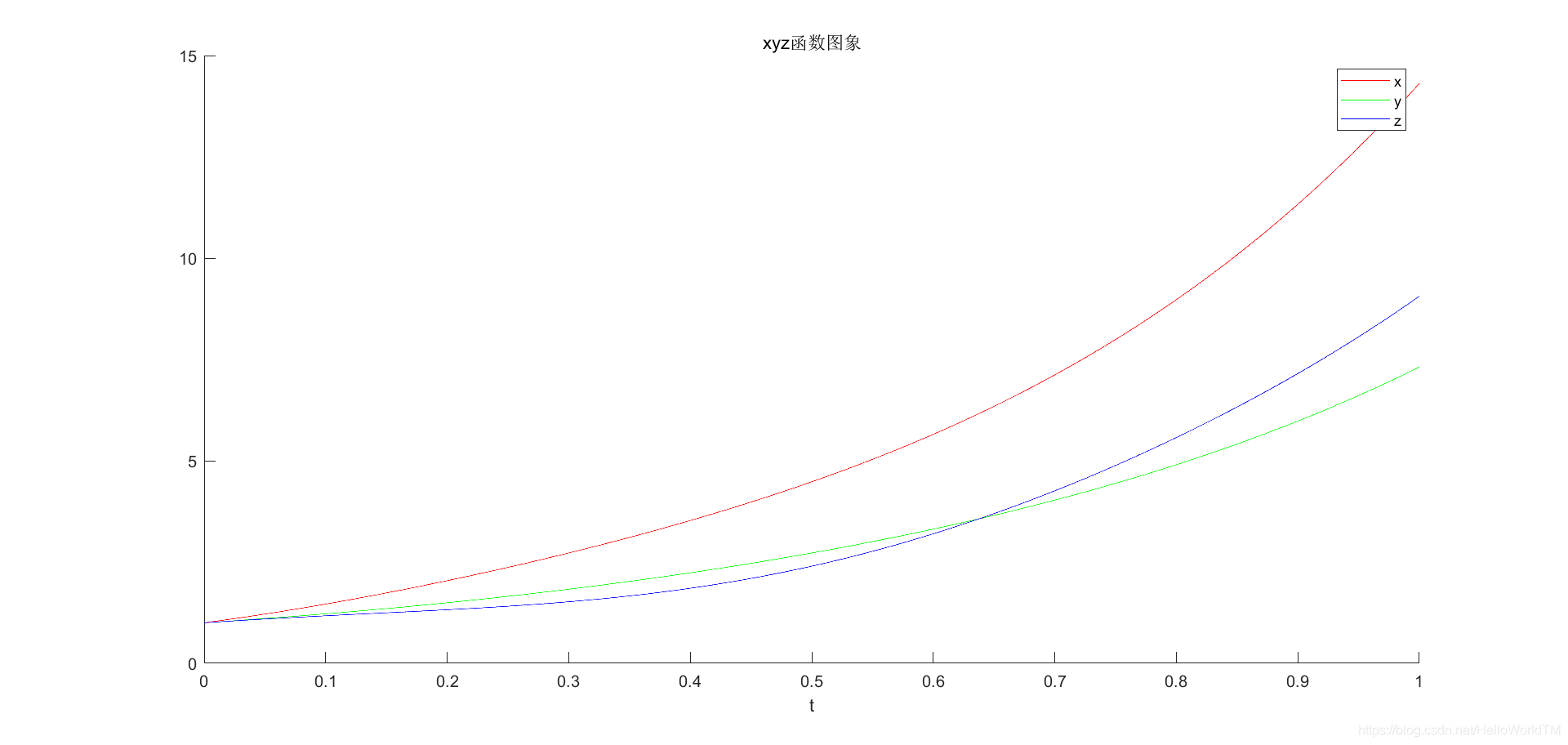
title('xyz函数图象');
hold off;

• 最后得到计算结果图象