一、kd树简介
kd树是一种树形结构,树的每个节点存放一个k维数据,某一节点的子节点可以看作是由过该节点一个平面切割后产生的(想象一下切蛋糕的过程),如此反复产生切割平面,就能为每个数据在空间中建立索引。如下图所示:

由于采用这种特殊的分割方式,使得在利用kd树做最近邻查找时,可以避开一些距离很远的点,查找速度得到了较大的提升,对于空间中N个k维数据,穷举法的算法复杂度为O(Nk),而使用kd树查找的算法复杂度只有O(klog(N))。kd树是一种典型的空间换时间的方式,即花费存储空间为数据建立索引,这样使得后续查找时速度更快,花费时间更少。
二、kd树生成
具体的算法实现主要参考的是这篇文章:https://www.cnblogs.com/eyeszjwang/articles/2429382.html,实现时有少量改动。生成kd树有两个关键的中间过程,即:
1.确定切分域
(1)确定split域:对于所有描述子数据(特征矢量),统计它们在每个维上的数据方差。以SURF特征为例,描述子为64维,可计算64个方差。挑选出最大值,对应的维就是split域的值。数据方差大表明沿该坐标轴方向上的数据分散得比较开,在这个方向上进行数据分割有较好的分辨率;
这段文字用通俗一点的语言来说就是:对于二维的情况,每一次做数据切分的时候,沿着x轴还是y轴做切分是一个问题,那么我们要怎么确定呢?我们可以统计这些二维数据的x值和y值的方差,方差越大说明数据在这一方向上越离散,而数据越离散说明沿着这一方向上数据之间的距离区分度越大,简单点来说就是相互之间隔得更远,我们就用这个方向做切分。
确定了切分域之后,我们就需要来对数据做切分了。
2.确定数据域
(2)确定Node-data域:数据点集Data-set按其第split域的值排序。位于正中间的那个数据点被选为Node-data。此时新的Data-set’ = Data-set\Node-data(除去其中Node-data这一点)。
简单来说,这句话的意思是:现在我们已经确定了沿着x轴做切分,那么我们要怎么决定在x轴哪里做切分呢?我们可以将所有数据根据x值的大小做一个排序,然后选取正中间那个数据的x值作为切分的位置。注意,这里有一个关键的问题是:如果我们有偶数个数据,怎么确定中间那个数据?难道我们选取中间两个数做一下平均???如果没有记错的话这应该是中位数的定义。。。如果这样完全就是自找麻烦!因为我们要确保至少有一个数据的x值落在切分点上,但是取平均之后并不能保证!!!所以更好的办法是,在有两个中间数据的情况下,随便选取一个数据的x值就行了。
决定了在x轴哪里做切分之后,我们就需要把数据做切分了,这里根据数据的x值相对于切分位置的大小,可以归为左节点和右节点,同时不要忘了:当前主节点也要保存一个数据,选取一个x值大小和切分位置相等的数据保存就行(如果有多个随便选一个就行,关键之处在于这个数据的x值落在切割线上。)
3.理解递归树
前面提到过,kd树是一种树形结构,因此可以递归生成,这是树形结构的共性,用程序语言来说,递归就是函数自己调用自己,在理解上也是很自然的。对于一组数据,我们通过找到的一个切分线把数据一分为二,而这个切分线的确定只和这组数据有关,左边的数据归为左节点,右边的数据归为右节点,更进一步,对于左边或者右边的这组数据,我们又可以将其看作一个整体,找到一个切分线把它一分为二,这样将一组数据一分为二的过程反复进行,相当于这个过程函数不断地调用自身,最终生成二叉树,将所有的数据分开。
4.python实现递归树代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
|
import numpy as np
import matplotlib.pyplot as plt
class kdTree:
def __init__(self, parent_node):
'''
节点初始化
'''
self.nodedata = None
self.split = None
self.range = None
self.left = None
self.right = None
self.parent = parent_node
self.leftdata = None
self.rightdata = None
self.isinvted = False
def print(self):
'''
打印当前节点信息
'''
print(self.nodedata, self.split, self.range)
def getSplitAxis(self, all_data):
'''
根据方差决定分割轴
'''
var_all_data = np.var(all_data, axis=0)
if var_all_data[0] > var_all_data[1]:
return 0
else:
return 1
def getRange(self, split_axis, all_data):
'''
获取对应分割轴上的中位数据值大小
'''
split_all_data = all_data[:, split_axis]
data_count = split_all_data.shape[0]
med_index = int(data_count/2)
sort_split_all_data = np.sort(split_all_data)
range_data = sort_split_all_data[med_index]
return range_data
def getNodeLeftRigthData(self, all_data):
'''
将数据划分到左子树,右子树以及得到当前节点
'''
data_count = all_data.shape[0]
ls_leftdata = []
ls_rightdata = []
for i in range(data_count):
now_data = all_data[i]
if now_data[self.split] < self.range:
ls_leftdata.append(now_data)
elif now_data[self.split] == self.range and self.nodedata == None:
self.nodedata = now_data
else:
ls_rightdata.append(now_data)
self.leftdata = np.array(ls_leftdata)
self.rightdata = np.array(ls_rightdata)
def createNextNode(self,all_data):
'''
迭代创建节点,生成kd树
'''
if all_data.shape[0] == 0:
print("create kd tree finished!")
return None
self.split = self.getSplitAxis(all_data)
self.range = self.getRange(self.split, all_data)
self.getNodeLeftRigthData(all_data)
if self.leftdata.shape[0] != 0:
self.left = kdTree(self)
self.left.createNextNode(self.leftdata)
if self.rightdata.shape[0] != 0:
self.right = kdTree(self)
self.right.createNextNode(self.rightdata)
def plotKdTree(self):
'''
在图上画出来树形结构的递归迭代过程
'''
if self.parent == None:
plt.figure(dpi=300)
plt.xlim([0.0, 10.0])
plt.ylim([0.0, 10.0])
color = np.random.random(3)
if self.left != None:
plt.plot([self.nodedata[0], self.left.nodedata[0]],[self.nodedata[1], self.left.nodedata[1]], '-o', color=color)
plt.arrow(x=self.nodedata[0], y=self.nodedata[1], dx=(self.left.nodedata[0]-self.nodedata[0])/2.0, dy=(self.left.nodedata[1]-self.nodedata[1])/2.0, color=color, head_width=0.2)
self.left.plotKdTree()
if self.right != None:
plt.plot([self.nodedata[0], self.right.nodedata[0]],[self.nodedata[1], self.right.nodedata[1]], '-o', color=color)
plt.arrow(x=self.nodedata[0], y=self.nodedata[1], dx=(self.right.nodedata[0]-self.nodedata[0])/2.0, dy=(self.right.nodedata[1]-self.nodedata[1])/2.0, color=color, head_width=0.2)
self.right.plotKdTree()
test_array = 10.0*np.random.random([30,2])
my_kd_tree = kdTree(None)
my_kd_tree.createNextNode(test_array)
my_kd_tree.plotKdTree()
|
这里代码中使用了Python面向对象技术,kdTree类的重要参数和前面给出的参考文章中的参数大致相同,具体代码细节不再说明,这里随机生成了30个范围在0-10之内的2维数据作为测试数据,下图是一次运行得到的结果:
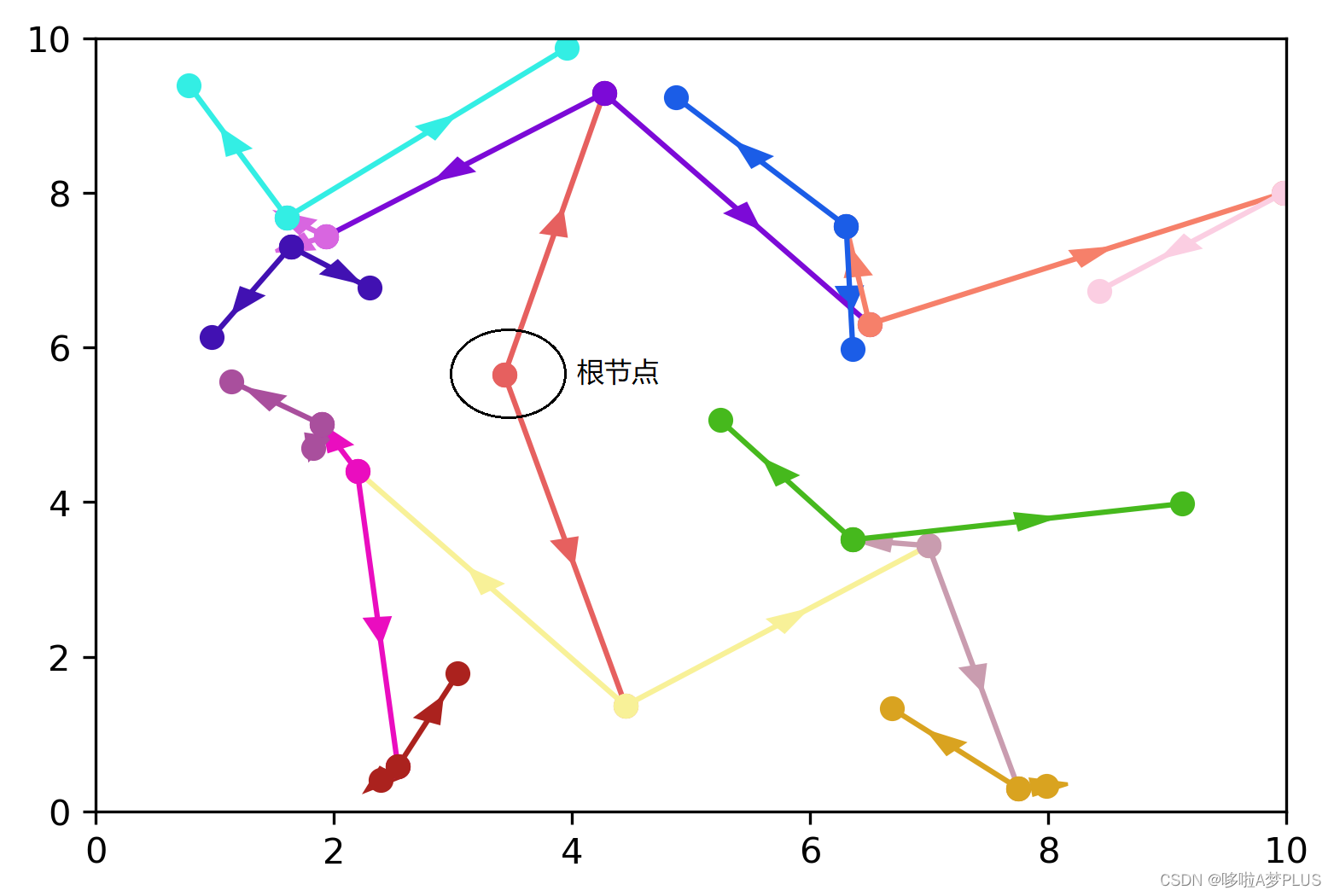
可以很容易看到中间橙色的点就是根节点,以及每个节点的迭代过程,运行过程无误。
三、kd树上的最近邻查找算法
加快对目标数据的最近邻数据的搜索过程,是kd树这种特殊存储结构的最主要功能,尤其是在数据量非常大时,其速度优势更加明显。kd树上的最近邻查找算法主要涉及两个过程,即:
1.生成搜索路径
这一过程相对容易,也很好理解。由于我们之前已经根据不同的切分线,生成了包含所有数据点的kd树,那么现在给我们一个新的数据,我们首先当然是根据这些切分线来判断待查找的数据是属于哪个分区的,我们当然有理由相信与这个数据同属一个分区的数据点(即某个叶节点)是其最近邻点的概率比不同分区的点的概率要大。因此,我们通过对目标数据的二叉查找,可以确定出一条搜索路径以及初始的最近邻点,但是要注意的是,通过二叉查找找到的叶节点是目标点的最近邻点的可能性较大,但不是一定的,如下图:
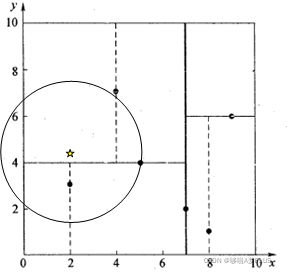
目标点落在了y=4的上半平面,但是其最近邻点却在y=4的下半平面,所以这里我们初步搜索出来的一个叶节点并不一定是目标点的最近邻点,我们还需要不断地沿着搜索路径回溯,确定同一主节点的其它子节点中是否存在与目标点距离更近的点。
2.搜索路径回溯
为了实现路径回溯的功能,这里需要使用栈来存储搜索路径,具体说来,当回溯到某一节点的父节点时,需要判断目标点到该父节点对应切分线的距离是否小于当前的最小距离,如果比最短距离还小,说明在该父节点对应的另一分支中有可能存在与目标点距离更小的点,因此就需要搜索该分支中的节点。
为了更加形象地说明,还是以上图为例。首先通过二分查找我们确定目标点与(4,7)点落在同一域内,因此将(4,7)作为初始最近邻点,然后向上回溯到(5,4)点,而(5,4)点对应的切分线是y=4,通过计算发现目标点到直线y=4的距离小于当前最短距离,因此在目标点的对侧即(5,4)节点的另一分支可能存在与目标点距离更近的点,因此我们需要跳到另一分支中重新检索,这里由于另一分支的深度不一定和前一分支相同,因此在跳到另一分支的头节点之后,我们还需要在此基础之上重复第1步中的路径搜索过程,到达该分支的叶节点,然后重复向上回溯查找直到将搜索路径全部回溯完成,我们就可以得到目标点的最近邻点。
这其中还有一个值得注意的地方,就是向上回溯时为了避免路径在两个分支之间来回跳跃导致死循环,需要将整个回溯过程中访问过的节点从路径中去掉,用一个标签来指示就可以,上述代码中使用的是isinvted来标记当前节点是否被访问过。
3.最近邻查找算法代码
具体代码实现是在以上kdTree类的基础上在添加几个内部函数就可以了,具体添加的函数为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| def divDataToLeftOrRight(self, find_data):
'''
根据传入的数据将其分给左节点(0)或右节点(1)
'''
data_value = find_data[self.split]
if data_value < self.range:
return 0
else:
return 1
def getSearchPath(self, ls_path, find_data):
'''
二叉查找到叶节点上
'''
now_node = ls_path[-1]
if now_node == None:
return ls_path
now_split = now_node.divDataToLeftOrRight(find_data)
if now_split == 0:
next_node = now_node.left
else:
next_node = now_node.right
while(next_node!=None):
ls_path.append(next_node)
next_split = next_node.divDataToLeftOrRight(find_data)
if next_split == 0:
next_node = next_node.left
else:
next_node = next_node.right
return ls_path
def getNestNode(self, find_data, min_dist, min_data):
'''
回溯查找目标点的最近邻距离
'''
ls_path = []
ls_path.append(self)
self.getSearchPath(ls_path, find_data)
now_node = ls_path.pop()
now_node.isinvted = True
min_data = now_node.nodedata
min_dist = np.linalg.norm(find_data-min_data)
while(len(ls_path)!=0):
back_node = ls_path.pop()
if back_node.isinvted == True:
continue
else:
back_node.isinvted = True
back_dist = np.linalg.norm(find_data-back_node.nodedata)
if back_dist < min_dist:
min_data = back_node.nodedata
min_dist = back_dist
if np.abs(find_data[back_node.split]-back_node.range) < min_dist:
ls_path.append(back_node)
if back_node.left.isinvted == True:
if back_node.right == None:
continue
ls_path.append(back_node.right)
else:
if back_node.left == None:
continue
ls_path.append(back_node.left)
ls_path = back_node.getSearchPath(ls_path, find_data)
now_node = ls_path.pop()
now_node.isinvted = True
now_dist = np.linalg.norm(find_data-now_node.nodedata)
if now_dist < min_dist:
min_data = now_node.nodedata
min_dist = now_dist
print("min distance:{} min data:{}".format(min_dist, min_data))
return min_dist
def getNestDistByEx(self, test_array, find_data, min_dist, min_data):
'''
穷举法得到目标点的最近邻距离
'''
data_count = test_array.shape[0]
min_data = test_array[0]
min_dist = np.linalg.norm(find_data-min_data)
for i in range(data_count):
now_data = test_array[i]
now_dist = np.linalg.norm(find_data-now_data)
if now_dist < min_dist:
min_dist = now_dist
min_data = now_data
print("min distance:{} min data:{}".format(min_dist, min_data))
return min_dist
|
代码的对齐格式是一致的,直接加入以上类中就可以,当然为了对比以及验证结果的正确性,在类中还实现了穷举查找算法。首先用50个点测试了一下回溯查找结果的正确性,绘制的结果如下:
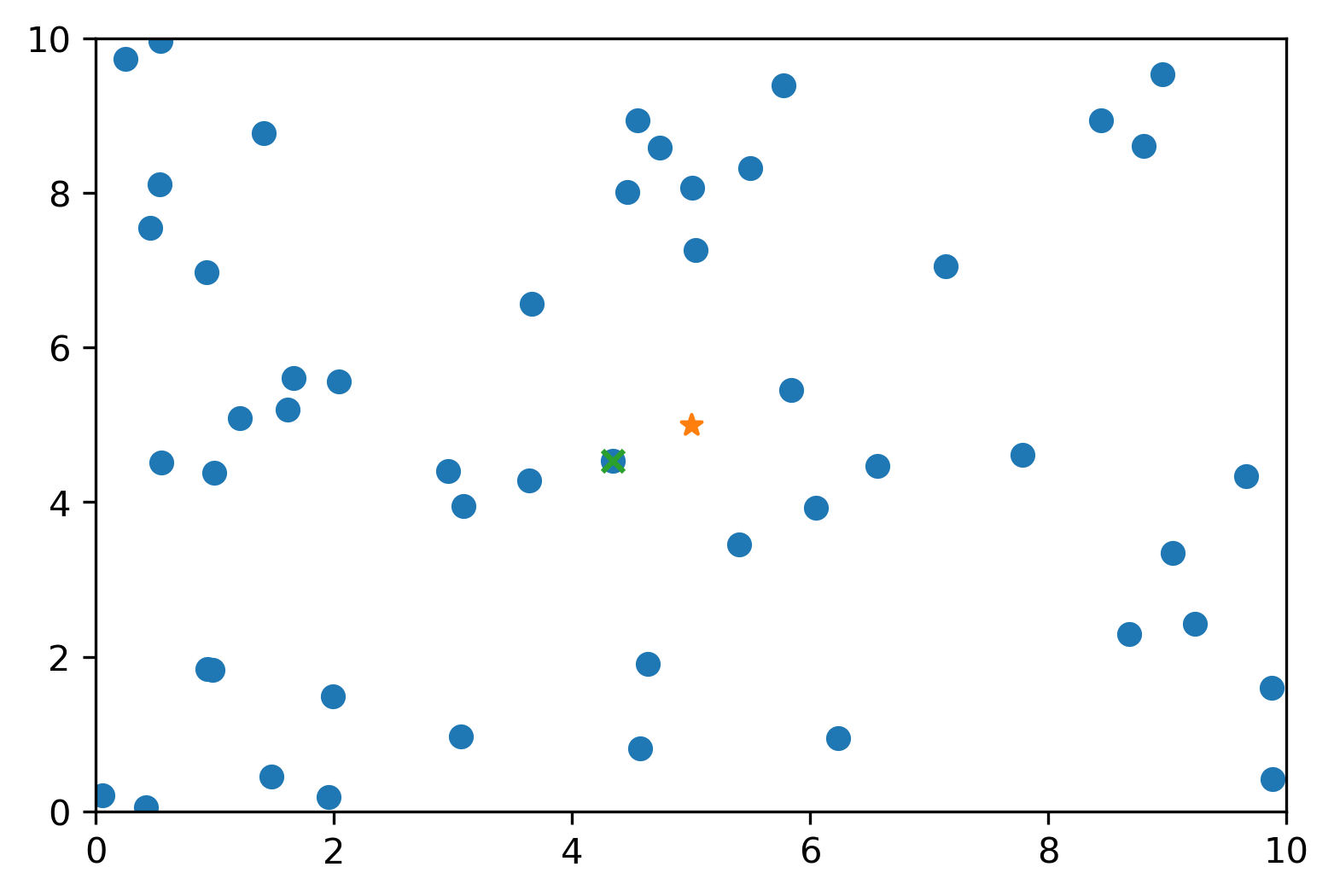
查找的目标点是(5.0, 5.0),查找到的最近邻点在目标点左下角,从图上来看结果是正确的。为了对比穷举法和利用kd树回溯查找的速度,数据点设置为10000个,代码为:
1
2
3
4
5
6
7
8
9
10
| test_array = 10.0*np.random.random([10000,2])
my_kd_tree = kdTree(None)
my_kd_tree.createNextNode(test_array)
find_data = np.array([5.0, 5.0])
min_dist = 0
min_data = np.array([0.0, 0.0])
%time min_dist = my_kd_tree.getNestNode(find_data, min_dist, min_data)
%time min_dist = my_kd_tree.getNestDistByEx(test_array, find_data, min_dist, min_data)
|
用%time命令来显示单步运行查找算法所需的时间,运行结果如下:

可以看到两种算法最终查找到的最短距离以及最近邻数据点都是一样的,证明了算法的正确性。同时kd树查找过程只用了1ms左右,而穷举法查找用了70ms左右,二者相差了70倍,当然随着数据量增大这个差距还会继续增加的,最终应该会趋于某个极限值。




