卷积与高斯滤波

Posted on 2024-06-05 Edited on 2024-06-06 In Share knowledges Views: Symbols count in article: 8.7k

一提到卷积，相信大部分人和我一样，首先想到的是时下非常火的一个机器学习算法——卷积神经网络（CNN）。实际上，即使自己之前看过相关的介绍，但是对于卷积操作一直是一知半解的状态，在充分查阅相关的资料后，打算整理成一篇博客，详细介绍卷积操作及其应用。

1. 理解卷积操作

1.1 卷积操作的数学定义

最早接触卷积操作，应该是在学习微积分时，教材中直接抛出卷积的定义：

对于两个函数 f(t) 和 g(t)，它们之间的卷积操作定义为：

f(t)\ast g(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau

尽管这个定义比较清晰，但是我们很难从中发掘出其背后的实际意义。下面让我们从概率论的角度挖掘卷积操作背后的内涵。

2.2 从概率论的角度理解卷积公式

设 X，Y 为两个独立变量，如果我们要计算 Z=X+Y 的概率，可以这样理解，对于每一个确定的 z，存在无数组 x、y 满足条件使得 x+y=z，因此我们需要将这些概率累积求和，如果 X 和 Y 是离散的变量，其概率分别为 $p_x(x)$ 和 $p_y(y)$ ，那么 Z=X+Y 的概率为：

p_z(z) = \sum^{\infty}_{x=-\infty}p_x(x)p_y(z-x)

对于 X 和 Y 是连续的情况，其概率密度函数分别是 $f_x(x)$ 和 $f_y(y)$ ，那么 Z=X+Y 的概率密度函数为：

f_z(z) = \int^{\infty}_{-\infty}f_x(x)f_y(z-x)dx

可以看到，以上两个公式正好是卷积的离散形式和连续形式的定义。因此，卷积操作与概率和统计中求独立随机变量的和完全等价。更加生动形象的例子可以参看丢骰子的例子，这里不再赘述。

2. 计算卷积

numpy 和 scipy 中都提供了卷积计算的相关函数定义，不同的是，scipy 中除了直接求和进行卷积计算之外，还提供了通过快速傅里叶变换的方式来计算卷积，这种方法对于较大尺寸的数组之间的卷积计算速度更快，其原理是卷积定理。下面将主要介绍 numpy 中卷积计算。

numpy.convolve 函数有三个输入参数，a,v 和 mode，其中 a 和 v 是输入矩阵，需要注意的一点是，官方文档中特别指出如果数组 v 的长度大于数组 a，那么在计算之前会交换两个数组，换句话讲，在计算的过程中始终保持数组 a 的长度大于数组 v。

2.1 `full` 模式

full 模式会计算数组 a 和 v 的所有卷积，其结果包含了所有可能重叠的部分，结果长度为：

length = len(a) + len(v) -1

示例代码和输出为：

import numpy as np

a = np.array([1, 2, 3, 4, 5])
v = np.array([0.0, 0.5, 1.0])
np.convolve(a, v, mode='full')

array([0. , 0.5, 2. , 3.5, 5. , 6.5, 5. ])

在输出数组的前两个和最后两个元素并不是a和v的所有元素卷积和，而只包含部分重叠部分求和。

2.2 `same` 模式

same 模式会返回与输入数组 a 长度相同的卷积结果，边界部分会被截断，即是：

length = len(a)

示例代码和输出：

import numpy as np

a = np.array([1, 2, 3, 4, 5])
v = np.array([0.0, 0.5, 1.0])
np.convolve(a, v, mode='same')

array([0.5, 2. , 3.5, 5. , 6.5])

2.3 `valid` 模式

valid 模式只会计算完全重叠部分的卷积，会直接舍弃不完全重叠的结果，其结果长度为：

length = len(a) - len(v) + 1

示例代码和输出为：

import numpy as np

a = np.array([1, 2, 3, 4, 5])
v = np.array([0.0, 0.5, 1.0])
np.convolve(a, v, mode='valid')

array([2. , 3.5, 5. ])

关于 numpy.convolve 函数的计算逻辑可以参看这篇博客：https://www.cnblogs.com/redtank/p/15678714.html。

3. 基于卷积的滑动窗口滤波算法

3.1 滑动窗口平均滤波

滑动窗口算法的原理是通过维护一个特定长度的窗口，使其在整个数组上移动，每次我们只操作窗口内部的数据，通过对窗口内数据采取特定的加权平均方式，可以实现滑动窗口滤波的效果。

卷积计算本质上正是一个滑动窗口的计算模型，在计算中，a 是整个数据，而 v 是滑动窗口，下面基于卷积计算来实现一个简单的滤波平均器。

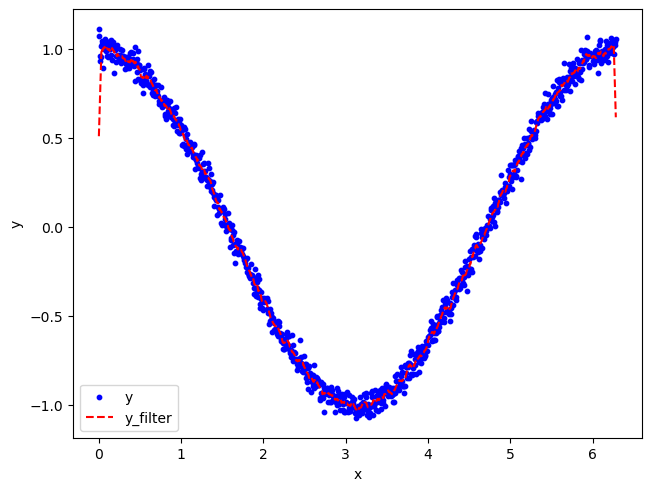
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, np.pi*2.0, 1000)
y = np.cos(x) + np.random.normal(0, 0.2, x.shape)*0.2
v = np.ones(10)
v = v/np.sum(v)
y_filter = np.convolve(y, v, mode='same')

fig, axs = plt.subplots(dpi=100, layout='constrained')
axs.scatter(x, y, marker='o', s=10, color='blue', label='y')
axs.plot(x, y_filter, color='red', linewidth=1.5, linestyle='dashed', label='y_filter')
axs.set_xlabel('x')
axs.set_ylabel('y')
axs.legend()

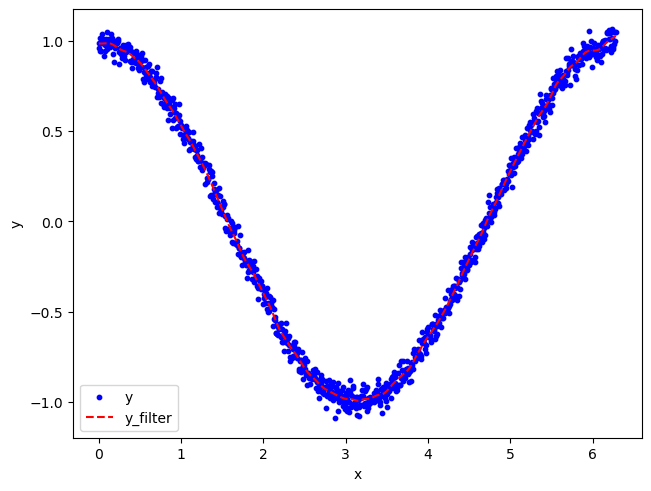
运行结果：
filter1

可以看到，经过滤波处理之后曲线的平滑度得到大大改善，基本能代表真实信号，在整个过程中，v 相当于是一个在输入信号 y 中滑动的窗口，对窗口内的数据进行加权平均操作产生过滤之后的信号，值得注意的是由于边缘效应，曲线的边缘部分并不能反映真实的情况，要解决这个问题，就需要对初始输入数据进行填充(padding)操作。

3.2 消除边缘效应

具体代码为：

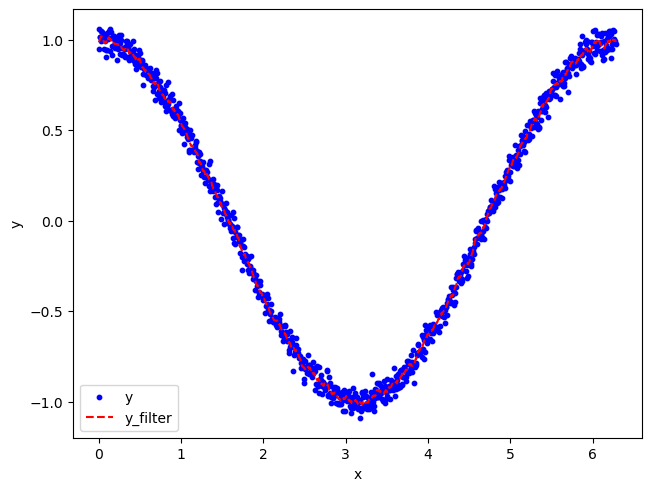
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, np.pi*2.0, 1000)
y = np.cos(x) + np.random.normal(0, 0.2, x.shape)*0.2
v = np.ones(10)
v = v/np.sum(v)
pad_width = (int((len(v)-1)/2.0), len(v)-1-int((len(v)-1)/2.0))
y_pad = np.pad(y, pad_width, mode='edge')
y_filter = np.convolve(y_pad, v, mode='valid')

fig, axs = plt.subplots(dpi=100, layout='constrained')
axs.scatter(x, y, marker='o', s=10, color='blue', label='y')
axs.plot(x, y_filter, color='red', linewidth=1.5, linestyle='dashed', label='y_filter')
axs.set_xlabel('x')
axs.set_ylabel('y')
axs.legend()

相较于之前的代码，上面代码中对输入数据 y 首先进行了 pad 操作，使用边缘值进行填充，并且需要保证填充之后的数据y_pad与v进行卷积之后得到的结果长度等于初始输入数据。以下为运行结果：

pad_filter2

可以看到在使用填充后的数据与 v 进行卷积操作之后，能够较好地消除边缘效应的影响，曲线的边缘部分基本也能够代表真实情况。

3.3 高斯滤波

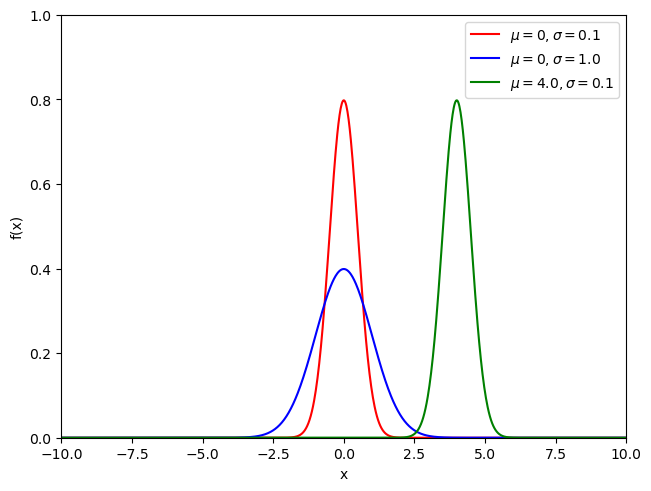
在上面的计算中，我们只是使用了最简单的取平均的方式来进行滤波，聪明的读者可能已经想到，如果我们更换窗口中数据加权平均的方式，不是就能构造出新的滤波器？高斯滤波就是这样产生的。提到高斯分布就必须要介绍一下高斯分布（正态分布），以往的实践和研究都表明，自然界中的大部分统计现象，都服从高斯分布，具体解释可以参看这篇博文：https://ruanyifeng.com/blog/2017/08/normal-distribution.html。对于一维高斯分布，其概率密度函数的形式为：

f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma ^2}}

其中 $\mu$ 是均值， $\sigma$ 是标准差，曲线关于 $x=\mu$ 中心对称，参看下图：

gaussian1d

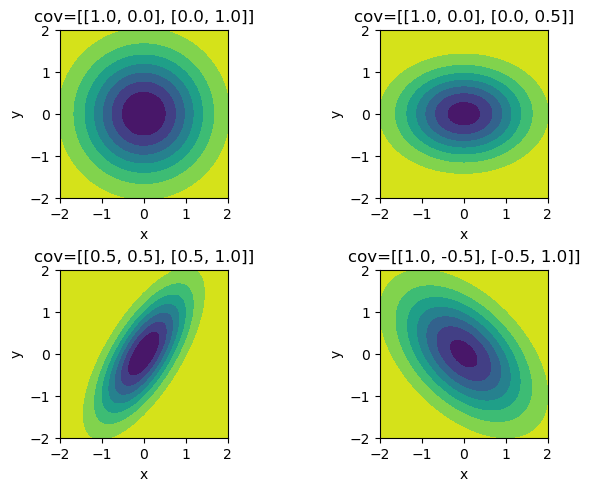
其中 $\mu$ 为函数的对称轴， $\sigma$ 越小，函数的峰越尖锐，峰值越小。对于多元高斯分布，参考scipy相关定义：https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.multivariate_normal.html#scipy.stats.multivariate_normal,

f(x) = \frac{1}{\sqrt{(2\pi)^kdet\sum}}e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}(x-\mu)}

其中 $\mu$ 是均值， $\sum$ 是协方差矩阵， $k$ 是 $\sum$ 的秩，对于二维的情况，参看下图：

gaussian2d

从上面可以总结出来，对于二维的情况，协方差矩阵的对角值决定椭圆ab轴的长度，而非对角值决定椭圆的倾斜度，这里需要注意的是要求协方差矩阵的半正定阵，对于二维的情况，需要满足：

C_{11} > 0 \quad\&\quad C_{11}C_{22}-C_{12}C{21}>0

言归正传，对于高斯滤波，核心思想是修改卷积过程中输入变量 v，使得从求普通平均变成求高斯平均，相关代码为：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

x = np.linspace(0, np.pi*2.0, 1000)
y = np.cos(x) + np.random.normal(0, 0.2, x.shape)*0.2

sigma = 1.0
v_size = int(6*sigma+1) ### (mu-3sigma, mu+3sigma)
mu = v_size//2
v_tmp = np.arange(v_size)
v= norm.pdf(v_tmp, loc=mu, scale=sigma)
v = v/np.sum(v)

pad_width = (int((len(v)-1)/2.0), len(v)-1-int((len(v)-1)/2.0))
y_pad = np.pad(y, pad_width, mode='edge')
y_filter = np.convolve(y_pad, v, mode='valid')

fig, axs = plt.subplots(dpi=100, layout='constrained')
axs.scatter(x, y, marker='o', s=10, color='blue', label='y')
axs.plot(x, y_filter, color='red', linewidth=1.5, linestyle='dashed', label='y_filter')
axs.set_xlabel('x')
axs.set_ylabel('y')
axs.legend()

结果为：

gaussianf1

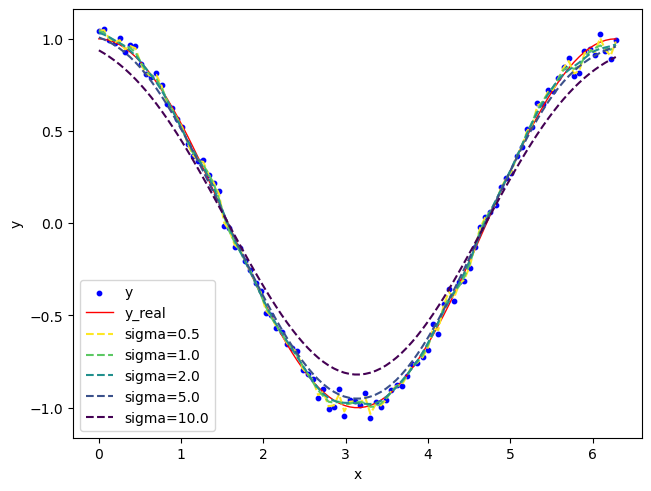
由于实践过程中误差的分布通常服从高斯分布，因此使用高斯滤波的效果通常是优于简单的平均滤波方式，下面是测试不同sigma大小对过滤结果的影响：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from scipy.stats import norm

x = np.linspace(0, np.pi*2.0, 100)
y = np.cos(x) + np.random.normal(0, 0.2, x.shape)*0.2

def get_v(sigma):
    v_size = int(6*sigma+1) 
    mu = v_size//2
    v_tmp = np.arange(v_size)
    v= norm.pdf(v_tmp, loc=mu, scale=sigma)
    v = v/np.sum(v)
    return v

def get_gaussian_filter(y, v):
    pad_width = (int((len(v)-1)/2.0), len(v)-1-int((len(v)-1)/2.0))
    y_pad = np.pad(y, pad_width, mode='edge')
    y_filter = np.convolve(y_pad, v, mode='valid')
    return y_filter

ls_sigma = [0.5, 1.0, 2.0, 5.0, 10.0]
ls_v = [get_v(sigma) for sigma in ls_sigma]
ls_y_filter = [get_gaussian_filter(y, v) for v in ls_v]

n_lines = len(ls_sigma)
cmap = mpl.colormaps['viridis_r']
ls_colors = cmap(np.linspace(0, 1, n_lines))
fig, axs = plt.subplots(dpi=100, layout='constrained')
axs.scatter(x, y, marker='o', s=10, color='blue', label='y')
axs.plot(x, np.cos(x), color='red', linewidth=1.0, label='y_real')
for i in range(len(ls_sigma)):
    axs.plot(x, ls_y_filter[i], color=ls_colors[i], linewidth=1.5, linestyle='dashed', label='sigma={}'.format(ls_sigma[i]))
axs.set_xlabel('x')
axs.set_ylabel('y')
axs.legend()

运行结果为:

gaussianf2

可以看到，通过调整sigma的大小，可以控制结果的平滑程度。

3.4 从一维扩展到多维高斯滤波

理解了以上一维的情况之后，很容易将算法扩展到更高维度，下面将以二维的情况为例。这里需要注意的一点是，numpy 中的 convolve 函数仅仅支持一维的卷积计算，要计算多维的情况，需要使用 scipy 中提供的 convolve 方法。下面给出代码：

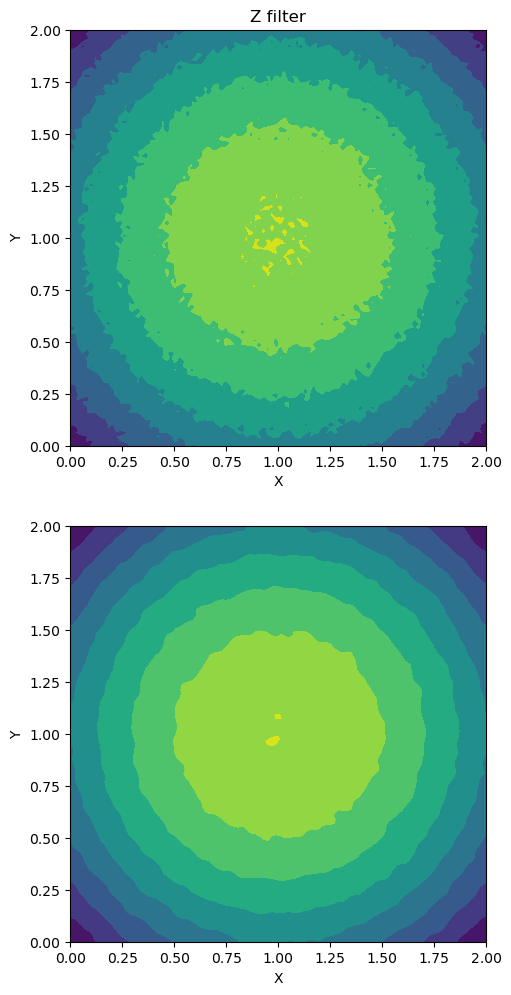
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from scipy.stats import multivariate_normal
from scipy.signal import convolve

x = np.linspace(0, 2.0, 100)
y = np.linspace(0, 2.0, 100)
X, Y = np.meshgrid(x, y)
Z = np.power(X-1.0, 2) + np.power(Y-1.0, 2) + 0.1*np.random.normal(scale=0.4, size=X.shape)

def get_v_2d(sigma1, sigma2):
    v_size1 = int(6*sigma1+1)
    v_size2 = int(6*sigma2+1)
    mu1 = v_size1//2
    mu2 = v_size2//2
    v = np.zeros((v_size1, v_size2))
    for i in range(v_size1):
        for j in range(v_size2):
            v[i, j] = multivariate_normal.pdf([i, j], mean=[mu1, mu2], cov=[[sigma1, 0.0], [0.0, sigma2]])
    v = v/np.sum(v)
    return v

def get_gaussian_filter_2d(y, v):
    pad_width1 = (int((v.shape[0]-1)/2.0), v.shape[0]-1-int((v.shape[0]-1)/2.0))
    pad_width2 = (int((v.shape[1]-1)/2.0), v.shape[1]-1-int((v.shape[1]-1)/2.0))
    y_pad = np.pad(y, (pad_width1, pad_width2), mode='edge')
    y_filter = convolve(y_pad, v, mode='valid')
    return y_filter

v = get_v_2d(1.0, 1.0)
Z_filter = get_gaussian_filter_2d(Z, v)

fig, axs = plt.subplots(ncols=1, nrows=2, dpi=100, layout='constrained', figsize=[5,10])
axs[0].contourf(X, Y, Z, level=50, cmap='viridis_r')
axs[0].set_xlabel('X')
axs[0].set_ylabel('Y')
axs[0].set_aspect('equal')
axs[0].set_title('Z')

axs[1].contourf(X, Y, Z_filter, level=50, cmap='viridis_r')
axs[1].set_xlabel('X')
axs[1].set_ylabel('Y')
axs[1].set_aspect('equal')
axs[0].set_title('Z filter')

下面为代码的运行结果：

gaussianf2d

参考资料：