势能函数简介

在网上翻到一篇讲势能函数的文章，内容比较基础，这里打算把全文翻译一下，文章链接：https://www.ks.uiuc.edu/Research/namd/2.9/ug/node22.html。

势能函数

在分子动力学模拟中，估算力是计算要求最高的部分，力是势能函数的负梯度，即：

$$\vec{F}(\vec{r})=-\vec{\nabla}U(\vec{r})$$

对于分子系统，势能函数包含求和：

$$U(\vec{r})=\sum U_{bonded}(\vec{r})+\sum U_{nonbonded}(\vec{r})$$

存在大量的成键项和非键项。成键项涉及共价键原子之间的2体、3体和4体相互作用，加和的复杂度是$O(N)$。非键项包含所有原子对之间的相互作用（通常需要排除已经参与了成键项的原子对），加和的复杂度是$O(N^2)$。快速评估技术已经能够很好地估算它们对于势能的贡献，计算成本为$O(N)$或$O(NlogN)$。

成键势能项

成键项涉及共价键原子之间的2体、3体和4体相互作用。
2体弹簧键势能描述了一对共价键原子(i,j)之间的谐振动，

$$U_{bond}=k(r_{ij}-r_0)^2$$

其中$r_{ij}=||\vec{r_j}-\vec{r_i}||$，给出了两个原子之间的距离，$r_0$是平衡距离，k是弹簧常数。

3体角度成键势描述了三个共价键原子(i, j, k)之间的角振动，

$$U_{angle}=k_{\theta}(\theta-\theta _0)^2+k_{ub}(r_{ik}-r_{ub})^2$$

其中，对于第一项,$\theta$是矢量$\vec{r}_{ij}=\vec{r}_j-\vec{r}_i$和$\vec{r}_{kj}=\vec{r_j}-\vec{r}_k$之间弧度制的夹角，$k_{\theta}$是角度角常数。第二项是Urey-Bradley项被用来描述端点处i和k原子之间的（非共价）弹簧作用，当常数$k_{ub}\neq0$时被激活，和两体弹簧键一样，$r_{ik}=||\vec{r}_k - \vec{r}_i||$给出了原子对之间的距离而$r_{ub}$代表平衡距离。

4体扭转角(也成为二面角)势描述了在一个连续键合的四元原子组(i,j,k,l)中，前三个原子组成的平面和后三个原子组成平面之间的二面角弹簧的相互作用，

$$U_{tors}=\begin{cases} k(1+cos(n\varphi+\phi)) & n>0, \\ k(\varphi-\phi)^2 & n=0. \end{cases}$$

其中$\varphi$是(i,j,k)面和(j,k,l)面之间的弧度制夹角，n为非负的整数，指示周期性。对于n>0，$\phi$代表相位偏移角，k为放大常数。对于n=0，$\phi$为平衡角，k的单位变为$potential/rad^2$。一个给定的四元原子组(i,j,k,l)可能有多个项对势能有贡献，每个都有它自己的参数。对扭转角使用多项允许势能函数产生复杂的角度变化，在截断傅里叶级数的计算中非常有效。

非键势能项

非键势能项包含所有(i,j)原子对之间的相互作用，通常不包括已包含在成键项中的原子。即使使用快速评估方法，计算非键势能的成本在MD模拟的每个时间步中仍然占主导作用。勒纳德-琼斯势描述了相隔较远原子间德弱极化吸引力，以及原子靠近时原子核之间的排斥力，

$$U_{LJ}=(-E_{min})[(\frac{R_{min}}{r_{ij}})^{12}-2(\frac{R_{min}}{r_{ij}})^6]$$

,其中$r_{ij}=||\vec{r}_j-\vec{r}_i||$给出了原子对之间的距离。参数$E_{min}=U_{LJ}(R_{min})$是势能项的最小值(Emin<0, 表明-Emin是井深)。随着$r_{ij}$的增加，LJ势快速趋于0，因此在超过截止半径时，通常把它截止（平滑移动）到0，消耗$O(N)$计算成本。
静电势对符号相同的原子电荷是排斥的，对符号相反的原子电荷是相互吸引的，

$$U_{elec}=\epsilon _{14}\frac{Cq_iq_j}{\epsilon _0 r_{ij}}$$

,其中$r_{ij}=||\vec{r_j}-\vec{r_i}||$给出了原子对之间的距离，而$q_i$和$q_j$是原子各自的电荷，对于所有的静电相互作用，库伦常数C和介电常数$\epsilon _0$是固定的。$\epsilon _{14}$是一个无单位比例因子，其值为1，但修改后的1-4相互作用除外，其原子对由三个共价键序列隔开（所以原子可能也参与了扭转角的相互作用），在这一情况下，$\epsilon _{14}=\mathcal{\epsilon}$，其中固定的参数$0\le\epsilon\le1$。虽然静电势也可以像LJ势那样用截止值来计算，但$1/r$势相比于$1/r^6$到达0的速度慢得多，因此忽略长程时的静电项会降低定性结果的可靠性，尤其是多电荷系统。还有其它一些快速计算方法可以近似计算长程静电项的贡献，需要$O(N)$或$O(NlogN)$的计算成本，取决于使用的方法。

接下来的部分介绍了非键相互作用，这部分来自这里：https://www.ks.uiuc.edu/Research/namd/2.9/ug/node23.html

非键相互作用

NAMD有很多参数可以控制计算非键相互作用的方式，这些参数是相互关联的，并且可能会非常难理解，因此本节将试图解释非键相互作用以及如何使用这些参数。

范德华相互作用

最简单的非键相互作用是范德华作用，在NAMD中，范德华相互作用通常在截止距离处被截断，即是cutoff参数。影响范德华相互作用的主要参数是switching，当该参数设置为on时，将使用平滑的转换函数在截止距离处平滑地截断范德华作用势。下图中显示了设置了转换函数平滑之后的范德华作用势能图，如果switching参数被设置为off，范德华能量会在截止距离处突然被截断，因此能量可能不守恒。

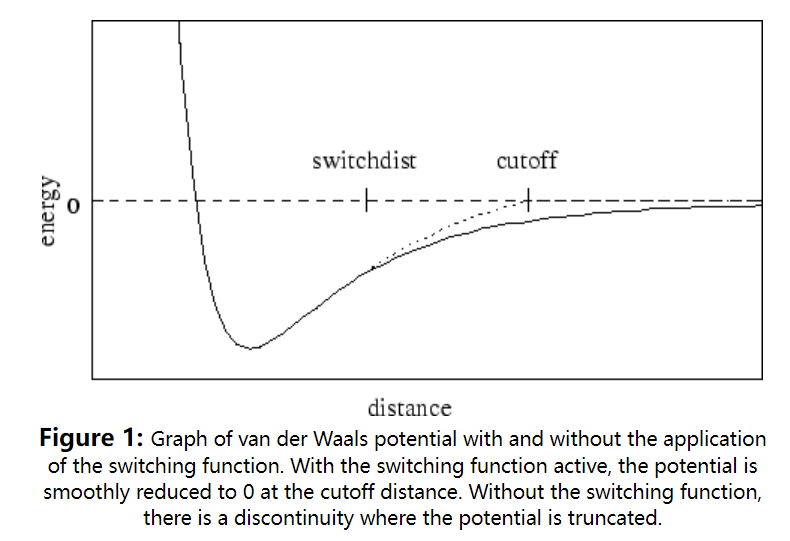
使用的转换函数是基于X-PLOR转换函数，参数switchdist指定使范德华势能平滑地变为0这一功能开始生效的距离，因此switchdist的值必须小于cutoff的值。

静电相互作用

静电的处理稍微复杂一点，因为在全静电相互作用中加入了多个时间步，有两种情况可以使用，一种是使用完整的静电相互作用，另一种是在给定距离处截断静电相互作用。

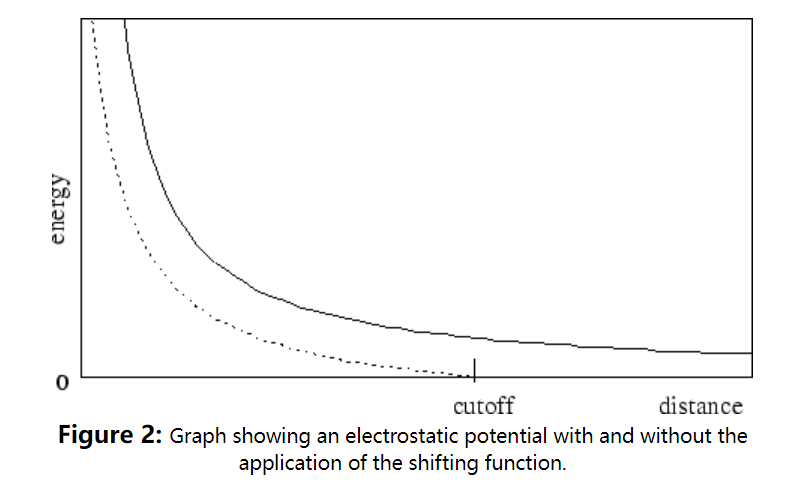
首先让我们考虑后一种情况：静电相互作用在截止距离处被截断。如果switching被开启，不是在截止距离处中断势能函数，而是对静电电势使用位移函数，如下图所示，位移函数移动整个势能曲线，使曲线在截止距离处于x轴相交，该位移函数基于X-PLOR使用的位移函数。

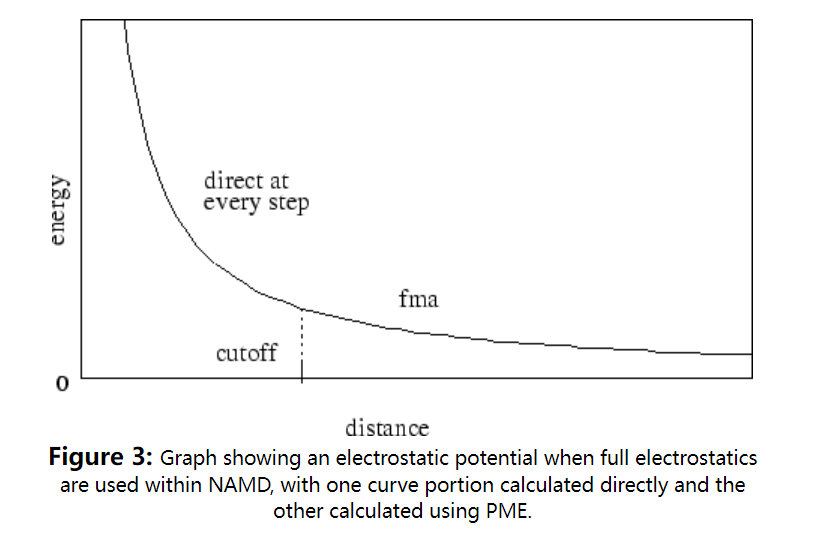
接下来，考虑计算全静电相互作用的情况，在这种情况下，静电相互作用在任何距离都不会被截断。在这一方案中，cutoff参数的含义有一点不同：它表示局部相互作用距离，或在该距离内，将在每个时间步中直接计算静电对的作用，在这一距离之外，只会以一定的周期计算相互作用，这些力将使用前面所述的多时间步积分方案来计算。