原子间的作用势综述----文献翻译

接上一篇文章，网上冲浪时翻到了这篇关于原子间作用势的综述，文章中对MD模拟中常用的EAM势做了详细的介绍，以及推导了一些常用的势场模型，推导过程较为详细，这里同样打算把全文翻译一下，注意：由于文章很长，所以翻译时可能会选择性的删掉一些内容，另外由于知识水平有限，文中可能存在错误，所有内容以原文为主，以下是原文链接：https://inis.iaea.org/search/search.aspx?orig_q=RN:38064873。

摘要

这篇报告给出了关于原子间作用势的综述。这篇综述并不完整，它只是想让读者了解原子间作用势的来源，以及为分子动力学应用中推导原子间势的一些常用方法提供基本思路。

我们首先在量子力学框架下简要介绍原子间势的概念，然后简要介绍推导半经验原子间势的常用方法。在对每种方法有了一些简单的概念之后，给出了一些常用势的使用参数，包括最新的一些势。尽管这些方法可以用到很多材料中，我们只讨论金属材料的实际情况。随后，讨论了使用一些广泛的修改方法如ad、hoc对一些常用方法的修改。本报告总结了多组分材料，尤其是金属合金的方法。

1.介绍

物质可以被描述为一个相互作用的原子系统，由相互作用的电子和原子核组成。这一整体必须用量子力学来描述，实际上，是泡利原子和电子-电子之间的相互作用阻止物质分解。

让我们假设一个固体或分子中总共包含$N_{at}$个原子和$N_{el}$个电子。那么系统随时间的演化可以通过总的多体波函数$|{\Psi_{tot}(t)}\rangle$，或者将总的波函数投影到坐标空间上$\Psi _{tot}(\vec{R}_1,...,\vec{R} _{Nat};\vec{r} _1,...,\vec{r} _{el};t)$,其中$\vec{R} _{\alpha}, \alpha = 1,...,N_{at}$,表示原子核的位置矢量，而$\vec{r} _i,i=1,...,N_{el}$,表示电子的位置矢量，t是时间变量。为了简单起见，这里忽略了电子的量子数，这种随时间演化的波函数可以通过含时薛定谔方程描述：

$$-i\hbar \frac{\partial}{\partial t}|{\Psi _{tot}(t)}\rangle =\hat{H}_{tot}|{\Psi _{tot}(t)}\rangle$$

该方程的形式解为：

$$|{\Psi _{tot}(t)}\rangle =e^{-\frac{i}{\hbar} \hat{H}_{tot}(t-t_0)}|{\Psi_{tot}(t_0)}\rangle$$

只有当$\hat{H}_{tot}$的所有本征值和本征态已知时，该结果才有意义，因此系统随时间的演化完全由定态薛定谔方程的本征方程决定：

$$\hat{H}_{tot}|{\Psi _{tot,n}}\rangle=E_{tot,n}|{\Psi _{tot,n}}\rangle , \forall n.$$

指数n代表可能的本征态，例如，基态和所有可能的激发态。为了简化，下面公式中指数n都省略了。

系统总的哈密顿量可以写为：

$$\hat{H}_{tot}=\hat{T}_N +\hat{T}_e+\hat{V}_{N-N}+\hat{V}_{e-e}+\hat{V}_{N-e}$$

其中$\hat{T}_N$表示对原子核的动能算符，$\hat{T}_e$表示对电子的动能算符，$\hat{V}_{N-N}$表示原子核之间库伦相互作用的势能算符，$\hat{V}_{e-e}$表示电子之间库伦相互作用的势能算符，$\hat{V}_{N-e}$表示电子和原子核之间相互作用的势能算符，将它们投影到坐标空间中，这些项的表达式为：

$$T_{N}(\vec{R}_1,...,\vec{R}_{N_{at}})=-\sum^{N_{at}}_{\alpha=1}\frac{\hbar ^2}{2M_{\alpha}}\nabla^2_{\vec{R}_{\alpha}}$$

$$T_{e}(\vec{r}_1,...,\vec{r}_{N_{el}})=-\sum^{N_{el}}_{i=1}\frac{\hbar ^2}{2m_{e}}\nabla^2_{\vec{r}_{i}}$$

$$V_{N-N}(\vec{R}_1,...,\vec{R}_{N_{at}})=\frac{1}{2}\sum^{N_{at}}_{\alpha =1}\sum^{N_{at}}_{\beta=1}\frac{Z_{\alpha}Z_{\beta e^2}}{4\pi \epsilon _0|\vec{R}_{\alpha}-\vec{R}_{\beta}|},\alpha \neq \beta$$

$$V_{e-e}(\vec{r}_1,...,\vec{r}_{N_{el}})=\frac{1}{2}\sum^{N_{el}}_{i =1}\sum^{N_{el}}_{j=1}\frac{e^2}{4\pi \epsilon _0|\vec{r}_{i}-\vec{r}_{j}|},i\neq j$$

$$V_{N-e}(\vec{R}_1,...,\vec{R}_{N_{at}};\vec{r}_1,...,\vec{r}_{N_{el}})=-\sum^{N_{el}}_{i=1}\sum^{N_{at}}_{\alpha =1}\frac{Z_{\alpha}e^2}{4\pi\epsilon _0|\vec{R}_{\alpha}-\vec{r}_i|}$$

其中原子核和电子的质量分别为$M_\alpha$和m，$Z_\alpha$是第α个原子的原子序数。

由于原子核的质量至少是电子质量的1000倍，因此将电子的运动和原子核的运动分开来处理是合理的，即我们假设电子能够随是跟上原子核的运动而运动，伯恩-奥本海默近似提出了这一假设，基于此我们可以总的多体量子态写作：

$$|{\Psi _{tot}}\rangle=|{\Psi _{at}}\rangle|{\phi_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})}\rangle$$

在这一假设中，电子的波函数在参数上只取决于原子的位置$\vec{R}_{\alpha}$,因此电子能够非常迅速地跟上原子核的运动，因此上面方程可以分为两部分：一部分描述电子态，一部分描述原子态。

$$\hat{H}_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})|{\phi_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})}\rangle=E_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})|{\phi_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})}\rangle$$

$$\hat{H}|{\Psi _{at}}\rangle=[E-E_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})]|{\Psi_{at}}\rangle$$

电子和原子核的哈密顿量表达式为：

$$\hat{H}_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})=\hat{T}_e+\hat{V}_{e-e}+\hat{V}_{N-e}(\vec{R}_1,...\vec{R}_{N_{at}})$$

$$\hat{H}_{at}=\hat{T}_N+\hat{V}_{N-N}$$

因此由于原子核和电子的相互作用，电子的哈密顿量和电子的本征方程仍然受到原子的位置这一参数决定，在坐标空间中可以写作：

$$\left[ -\sum^{N_{at}}_{\alpha=1}\frac{\hbar ^2}{2M_{\alpha}}\nabla^2_{\vec{R}_{\alpha}}+V_{IAP}(\vec{R}_1,...,\vec{R}_{N_{at}}) \right]\Psi_{at}(\vec{R}_1,...,\vec{R}_{N_{at}})=E\Psi _{at}(\vec{R}_1,...,\vec{R}_{N_{at}})$$

其中我们将原子间的作用势定义为：

$$V_{IAP}(\vec{R}_1,...,\vec{R}_{N_{at}})=\frac{1}{2}\sum_{\alpha,\beta}\frac{Z_{\alpha}Z_{beta}}{|\vec{r}_{\alpha}-\vec{r}_{\beta} |}e^2+E_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})$$

原子间的相互作用势$V_{IAP}(\vec{R}_1,...,\vec{R}_{N_{at}})$ 包含原子核之间库伦排斥作用以及所有的电子相互作用，与 $E_{el}(\vec{R}_1,...,\vec{R}_{N_{at}})$ 项有关。在本节结束时我们指出，在分子动力学模拟中，薛定谔方程通常被牛顿方程取代：

$$M_{\alpha}\frac{d^2\vec{R}_{\alpha}}{dt^2}=-\nabla_{\alpha}V_{IAP}(\vec{R}_1,...,\vec{R}_{N_{at}}),\alpha=1,...,N_{at}$$

下文中将致力于阐明一些在描述原子间作用力$V_{IAP}(\vec{R}_1,...,\vec{R}_{N_{at}})$时有用的近似。

2.原子间作用势

原则上，可以通过求解感兴趣原子位置上的电子薛定谔方程来计算原子间作用势，可以使用从头算技术如DFT、Hatree Fock方法(HF)、组态相互作用(CI)、耦合簇(CC)等来求解描述多体电子系统的薛定谔方程。所有的这些从头算技术会产生$N_{el}$个自洽场(SCF)方程，其参数仅取决于原子的位置。随着系统中电子数量的增加，求解自洽方程所需要的时间非常迅速地增加，因此这些技术很快会随着电子数量地增加变得难易处理。

正是由于这一原因，半经验的方法被提出来了，在这些方法中，一个根本性的尝试是通过实验或从头算的数据，来拟合原子间势函数(IAP)。下一节中我们将会聚焦在半经验原子势(Inter Atomic Potential,IAP)上。

2.1. 半经验原子间作用势

根据半经验原子作用势理论，我们想把具有$N_{at}$个原子的系统之间的相互作用的总能量，拆分为多体项能量的总和，通常我们可以得到：

$$E_{tot}=E_{0}+\frac{1}{2!}\sum_{\alpha, \beta}V_2(\vec{R}_{\alpha},\vec{R}_{\beta})+\frac{1}{3!}\sum _{\alpha, \beta, \gamma}V_3(\vec{R}_{\alpha},\vec{R}_{\beta},\vec{R}_{\gamma})+....$$

在这一表达式中，$E_0$表示参考能量(后面将省略),$V_n$表示描述n体相互作用的原子间的势函数，当只考虑对相互作用时，我们称为对势(pair potentials),当考虑多体之间的相互作用时，我们称为簇势(cluster potentials)。对势通常被设计为模拟一小类原子之间的重排，适用范围很窄。簇势通过考虑更多的相互作用来提高对势的精度，三体和更高阶项包含角度和化学键的信息，而对势不能描述这些。在实际操作中，簇势通常截止在三体水平(不考虑更高阶)。相较于对势方案，簇势方案可以在更宽范围处理原子构型，但是毫无疑问，它们与精确地描述全局能量$E_{tot}$这一目的相距很远，相较于使用对势，使用簇势所花费的时间增加了很多。

另一种展开原子间相互作用总能量的方法是：

$$E_{tot}=E_0+\frac{1}{2}\sum _{\alpha, \beta}V_2({\vec{R}_{\alpha},\vec{R}_{\beta}})+\sum _{\alpha}F[\sum_{\beta}g_2(\vec{R}_{\alpha},\vec{R}_{\beta}),\sum _{\beta , \gamma}g_3((\vec{R}_{\alpha},\vec{R}_{\beta}),\vec{R}_{\gamma}),...]$$

我们没有把原子间相互作用的总能表示为成对和更高阶的相互作用的总和，而是将更高阶相互作用描述为基于团簇项$g_n$的函数F。能量泛函F描述了与原子α相关的总能部分与函数$g_n$之间描述的局部环境之间的关系，如果描述局部环境的函数$g_n$仅限于成对相互作用，那么我们就称之为成对函数，如果保留了更高阶的相互作用项，那么我们就称之为簇函数，成对函数能够生成对势，并且能更好地描述非均匀环境。如果另外选择一个合适地截止半径，那么计算速度与对势大致相同。类似的，簇函数能够生成簇势，明确地将角向力加入到描述局域环境的函数中，簇函数的精度相较于对函数的精度提高了很多，并且相较于簇势，它们能更好地处理非均匀环境。团簇泛函通常仅限于三体和四体级别，因为在这些级别上原子几何结构仍然是可视化地，相较于更高阶的处理计算时间仍然很短。

因此半经验原子间的作用势主要可以分为四组：

1. 对势
2. 成对泛函
3. 簇势
4. 团簇泛函

接下来的章节一些推导半经验原子间作用势的主流方法和一些广泛使用的参数。

2.2对势

由于对势在簇势和团簇泛函中都会重新出现，因此给出一些这类势常用的显式形式是很有用的。

2.2.1排斥势阱

这类势被用来模拟相互作用势的排斥部分，这在小粒子(<1A)分离时是有效的,这类势在高能粒子的级联碰撞过程的模拟中起了很多作用。一种常用的排斥阱势是两体屏蔽库伦势，如下式：

$$V(r)=\frac{Z_1 Z_2 e^2}{4\pi \epsilon _0 r}\chi(x)$$

其中$x=r/a_0$,$a_0$是屏蔽长度，其定义为：

$$a_0=0.8853a_B\overline{Z}^{-1/3}$$

$\overline{Z}$是两个粒子的平均原子数，Firsov提出的形式为：

$$\overline{Z}^{-1/3}=(Z_1^{1/2}+Z_2^{1/2})^{-2/3}$$

Bohr也使用如下形式：

$$\overline{Z}^{-1/3}=(Z_1^{2/3}+Z_2^{2/3})^{-1/2}$$

基于此，屏蔽长度a0通常被用作SCF计算或实验数据的拟合参数。Firsov提出的$\chi$函数的形式是Thomas—Fermi方程的解：

$$x^{1/2}\frac{d^2\chi}{dx^2}=\chi ^{3/2}$$

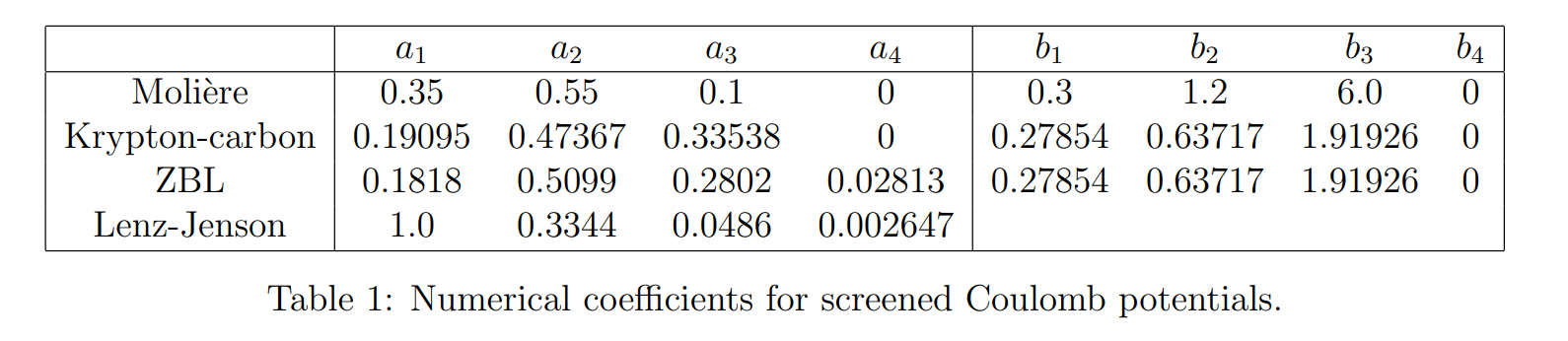
对于Moliere势、krypton-carbon势和ZBL势，$\chi$函数的形式如下：

$$\chi(x)=\sum_{i=1}^4a_{i}e^{-b_ix}$$

Lenz-Jenson势的形式为：

$$\chi(x)=e^{-q}(1+\sum_{i=1}^4a_iq^i),q=3.11126x^{1/2}$$

在所有的势中，$\chi$都满足Thomas Fermi方程的数值解，并且拟合的参数汇总在下表中：

在原子碰撞研究中，ZBL势是最常用的，因为和其它势相比，ZBL势具有更好的实验一致性。

另一种常用的排斥阱势的形式是Born-Mayer势，它的形式如下：

$$V(r)=Ae^{-br}$$

对于原子碰撞研究来说，这一势的结果不是太令人满意，因为每一对原子组合，A和b的值都必须独立确定。即使如此，这一势被证明在金属中（如铁）产生阈值位移能是有效的。这种形式的排斥势主要用于模拟某些粒子材料的近邻排斥作用，可以在这篇文章中找到相关的参数值：https://books.google.com/books?id=23rX2zjQG-QC&printsec=frontcover&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false

2.2.2吸引势阱

这些类型的势描述了1-4A左右粒子分离时相互作用势的吸引部分，这些类型的势的一个主要缺点是它们的适用范围非常有限，例如它们只能描述密堆积晶体结构，有两个广泛使用的类型：Lennard-Jones势和Morse势。

LJ势采用如下形式：

$$V(r)=4\epsilon\left[ (\frac{\sigma}{r})^{12}-(\frac{\sigma}{r})^6 \right]$$

这种势是用来表示惰性气体的，其前提是固态惰性气体中的原子在与它们在自由状态下所具有的稳定电子闭合壳层构型相比只有轻微的畸变。闭合壳层中电子构型的轻微畸变会产生偶极相互作用，其正比于$r^{-6}$。正是这种相互作用导致闭壳原子间产生了范德华力。对于更短的距离，原子之间的电子壳层开始发生重叠，由于泡利不相容原理，两个原子之间会产生很强的排斥力，正比于$r^{-12}$。在这一形式中，$2^{1/6}\sigma$是平衡距离，而ε是阱深，这些参数都能根据从头算得到的数据拟合。

Morse势的形式是：

$$V(r)=\frac{D_e}{S-1}[e^{-(2S)^{1/2}\beta(r-R_e)}-Se^{-(2/S)^{1/2}\beta(r-R_e)}]$$

在其原始形式中，参数S被设置为2。剩下的三个拟合参数分别是：二聚体能量$D_e$,平衡位移$R_e$和一个额外的参数β，它通常可以拟合为材料的体积模量，以上形式中S是一个额外的拟合参数。

2.2.2.3重叠势

在研究宽能量窗口内的原子间散射时，如级联碰撞过程，应该使用既描述内聚、成键又描述排斥的势。这种情况的一个可能解决方案是在数值上合并一个吸引势阱和一个排斥势阱。在过渡区间，可以用三次样条曲线来拟合，总的来说最终的势能应该具有如下形式：

$$V(r)=\begin{cases} Repulsive-well &0<r<r_a \\ Cubic-spline &r_a\le r \le r_b \\ Attractive-well &r_b \le r \end{cases}$$

其中对于$r_a$和$r_b$的选择存在一定的灵活性，但是通常来讲这些参数必须在一开始就固定下来。值得注意的是，在过渡区间，尽管大多数时候三次样条曲线可以平滑地把不同势链接起来，但是在某些情况下势能曲线的连接区域也可能产生震荡，这些非物理的震荡始终应该避免，因为级联碰撞过程在重叠区域通常是很敏感的。

2.3对势的经验拓展

在这一小节中，我们将会阐述对于Morse形势的一个专门扩展，这一扩展的目的是在不使用经典的多体展开的情况下考虑(键)角对势能的贡献。这一扩展是Tersoff首先提出来的，他在对势中引入了一个与环境有关的键参量，即键强，这一势可以写作：

$$V(R_{\alpha \beta})=f_{C}(R_{\alpha \beta})[a_{\alpha \beta}f_R(R_{\alpha \beta})+b_{\alpha \beta}f_A(R_{\alpha \beta})]$$

其中$R_{\alpha \beta}$是原子α和原子β之间的距离，$f_R$函数表示排斥对势，$f_A$是吸引对势，额外项$f_C$只是一个平滑的截止函数用来限制势函数的范围。这一势唯一新颖的地方是，相关系数$b_{\alpha \beta}$现在变成了关于局域环境的函数，它表示的是键序的一种度量，并被定义为原子α和β配位的单调递减函数，函数$a_{\alpha \beta}$仅由范围限制项组成。

对于$f_{R}(r)$和$f_A(r)$，采用指数函数形式：

$$f_R(r)=Aexp(-\lambda _1r)$$

$$f_A(r)=-Bexp(-\lambda _2r)$$

截止函数的形式如下：

$$f_C(r)=\begin{cases} 1 &r \lt R-D \\ \frac{1}{2}-\frac{1}{2}sin\left( \frac{\pi}{2}(r-R)/D \right) &R-D\lt r \lt R+D \\ 0 &r\gt R+D \end{cases}$$

该函数具有连续的取值，并且所有的r处都可导，在R附近函数的取值从1到0(R为截止半径)。包含键角贡献的函数$b_{\alpha \beta}$具有如下形式：

$$b_{\alpha \beta}=(1+\beta ^n \zeta ^n _{\alpha \beta})^{-1/2n}$$

$$\zeta _{\alpha \beta}=\sum _{\gamma \ne \alpha,\beta}f_C(R_{\alpha \beta})g(\theta _{\alpha \beta \gamma})exp\left[ \lambda^3_3(R_{\alpha \beta}-R_{\alpha \gamma})^3 \right]$$

$$g(\theta)=1+c^2/d^2-c^2/[d^2+(h-cos\theta)^2]$$

其中$\theta _{\alpha \beta \gamma}$是αβ键和αγ键之间的键角，注意$b_{\alpha\beta}\neq b_{\beta \alpha}$。有效配位函数$\zeta_{\alpha \beta}$考虑了不同近邻原子之间的相对距离和键角。对于$a_{\alpha \beta}$函数建议采用以下形式：

$$a_{\alpha \beta}=(1+\kappa^n\eta^n_{\alpha \beta})^{-1/2n}$$

$$\eta_{\alpha \beta}=\sum_{\gamma \neq \alpha , \beta}f_C(R_{\alpha \beta})exp\left[ \lambda^3_3(R_{\alpha \beta}-R_{\alpha \gamma})^3 \right]$$

在这一表达式中κ取得足够小以致于$a_{\alpha \beta}\approx 1$。这类势最初是用来描述半导体的，但最近又重新引起了人们的兴趣，尝试用它来描述金属间化合物。

2.4嵌入原子势(EAM)

嵌入原子势起源于DFT，Hohenberg和Kohn定理指出：总的电荷密度唯一地决定了外加参数下的外势场，并且反之亦然。作为这个定理的结果，Stott-Zaremba推论指出：杂质的嵌入能由添加杂质前主体系统的电子密度决定。

这个推论可以这样理解：没有受到干扰的主体系统的势由其电荷密度决定，当引入杂质后，总的势能是主体势能和杂质势能的加和，因此含有杂质的主体的能量是主体势能和杂质势能的泛函。由于主体的电荷密度和杂质势能仅由杂质原子核的位置和电荷决定，因此带有杂质的主体的能量是未受干扰主体的电子密度的泛函，也是杂质类型和位置的泛函。总能可以写作：

$$E=\mathcal{F} _{Z,R}[\rho_h(r)]$$

其中$\rho_h(r)$是未受干扰的主系统的电荷密度，而Z和R分别是杂质的类型和位置。泛函$\mathcal{F}$的形式是通用的，与主系统无关，但是它的形式未知。

一种简答的近似方法是假设能量仅取决于杂质周围有限的环境，或者相当于假设杂质感受到的是周围均匀的电子密度，这种近似称为准原子近似，这种简化既可以看作是局域近似，也可以看作是涉及密度函数连续梯度的最低阶项。

由于每个原子都可以被看作其它主体原子中的杂质，因此在准原子近似下，总能量可以写作：

$$E=\sum_{\alpha}F_{\alpha}[\overline{\rho}_{\alpha}]$$

其中F是嵌入能而$\overline{\rho}_{\alpha}$是位置$\vec{R}_{\alpha}$处没有α原子时主体系统的平均电荷密度。需要注意的是，嵌入函数F与泛函$\mathcal{F}$不同。由于极端局域性的假设，以及电子气和背景的完全均匀性，导致了结果不够真实。为了正确地描述能量，需要添加原子核和原子核之间的排斥作用，在这里假设核之间以短程成对排斥的形式存在。

当选定了一个合适的截止半径之后，EAM能量的计算耗时与对势的计算时间大致相同。总能变为：

$$E_{tot}=\frac{1}{2}\sum _{\alpha,\beta}V(R_{\alpha \beta})+\sum_{\alpha}F[\overline{\rho}_{\alpha}]$$

其中$F[\overline{\rho}_{\alpha}]$是嵌入函数，$\overline{\rho}_{\alpha}$是原子电荷密度的叠加：

$$\overline{\rho}_{\alpha}=\sum_{\beta}\rho(R_{\alpha \beta})$$

原子电荷密度函数$\rho(R_{\alpha \beta})$仅与原子α和原子β之间的距离有关。注意如果嵌入函数$F[\rho]$有如下形式：

$$F[\rho]=-A\rho ^{-1/2}$$

我们的数学表达式与紧束缚模型中的二阶矩阵的近似表达式相同(见第2.5节)。通常来说，$F[\rho]$没有预先定义的函数形式，它的形式在拟合的过程中确定。

Daw和Baskes将嵌入函数拟合为$\overline{\rho}_{\alpha}$和$\rho(R_{\alpha \beta})$的函数，其中$\rho(R_{\alpha \beta})$的形式为：

$$\rho(R_{\alpha \beta})=\frac{Z_\alpha Z_\beta}{R_{\alpha \beta}},Z(r)=Z_0(1+\gamma r^\kappa)e^{-vr}$$

其中γ、κ和v是可调参数，$Z_0$是价电子数。

Voter-Chen对类氢的4s轨道采用的密度泛函形式为：

$$\rho(r)=r^6(e^{-\beta r}+2^9e^{-2\beta r})$$

Foiles给出的密度泛函的形式为：

$$\rho(r)=r^8(e^{-\beta r}+2^{11}e^{-2\beta r})$$

对于Johnson方法，嵌入函数的普遍形式为：

$$F[\rho]=-F_0\left[ 1-nln(\frac{\rho}{\rho ^{eq}}) \right]\left( \frac{\rho}{\rho ^{eq}} \right) ^n$$

其中$\rho ^{eq}$是体系达到平衡时的电荷密度ρ，$F_0$和n可以通过下式计算：

$$F_0=E_c-E_f$$

$$n=\sqrt{\frac{\Omega B}{A \beta ^2 E_f}}$$

其中$E_c$是每个元素的结合能，$E_f$是单个空位的形成能，Ω是平衡时的原子体积，B是体模量，$A=2C_{44}/(C_{11}-C_{12})$，表示各向异性比，参数化的密度函数形式为：

$$\rho (r)=\rho _e \left( \frac{r_1}{r} \right)^{\beta}$$

对于所有的过渡bcc金属，参数β取6，参数$\rho _e$是最近邻原子的电荷密度分布值(这里取1)。

2.5紧束缚方法

对于紧束缚方法，“半经验”的说法是合适的，因为以上方程中描述的“嵌入”能量的函数F的形式将使用第一性原理的近似来推导。为了获得函数形式，我们首先还是聚焦在伯恩-奥本海默近似上，通过使用上面提到的从头算中的技术之一来求解电子薛定谔方程。这些技术将电子薛定谔方程简化为$N_{el}$个单电子的SCF方程，即每个方程描述一个电子，这样，电子态就可以展开成分子轨道的线性展开：

$$|\Phi _{el}(\vec{R}_1,...,\vec{R}_{N_{at}}) \rangle = \sum_{s}a_s| \psi(\vec{R}_1,...,\vec{R}_{N_{at}}) \rangle$$

其中s代表分子轨道(MO)，$a_s$为展开系数。注意在这一框架中，每个MO都与所有原子核相关联，换句话说，电子是离域的，每个分子轨道被两个自旋反平行的电子占据，因此指标s覆盖了$N_{el}/2$个分子轨道。

在紧束缚方法中，一种是将分子轨道近似为原子轨道的线性组合(LCAO):

$$|\psi_s(\vec{R}_1,...,\vec{R}_{N_{at}})\rangle = \sum_{\alpha}\sum_{\sigma}b^{(s)}_{\alpha \sigma}|\phi_{\sigma}(\vec{R}_\alpha)\rangle$$

其中σ代表一个原子轨道，$b^{(s)}_{\alpha \sigma}$是与分子轨道相关的的展开系数，在这种假设下，每个电子都与一个特定的原子相关联，换句话说，电子现在是定域化的，每个原子轨道被两个自旋反平行的电子所占据，LCAO近似下的电子态现在变成：

$$|\Phi _{el}(\vec{R}_1,...,\vec{R}_{N_{at}})\rangle = \sum_{\alpha}\sum_{\sigma}(\sum_{s}a_sb^{(s)}_{\alpha \sigma})|\phi_{\sigma}(\vec{R}_\alpha)\rangle=\sum_{\alpha}\sum_{\sigma}c_{\alpha \sigma}|\phi_{\sigma}(\vec{R}_{\sigma})\rangle$$

其中指标σ会遍历所有的原子轨道，通过求解LCAO近似下的电子问题，我们得到了简并度为2的$N_{el}/2$个不同束缚单粒子能级，每个分子轨道上有两个自旋反平行的自旋电子。请注意，MO通常形成一个完整的正交集，而AO通常形成的是完整但不正交的集合，这是因为不同的AO位于不同的原子核上，基于能级$\epsilon_s$我们可以将能带能量$E_{band}$定义为所有占据能级的叠加：

$$E_{band}=2\sum_s n_s \epsilon _s$$

其中$n_s$表示分子轨道的占据数，如果轨道s是占据的，其值为1，如果是非占据的，其值为0，基于这些结果我们写出态密度的(分子轨道的能量分布)表达式:

$$D(\epsilon)=\sum _s \delta(\epsilon-\epsilon _s)=\sum _{\alpha \sigma}D_{\alpha \sigma}(\epsilon)$$

在第二行中，我们认为$D(\epsilon)$是系统中每个原子轨道的局域态密度的总和，如果局域态密度由下式给出，这一条件是满足的：

$$D_{\alpha \sigma}(\epsilon)=\sum _s|\langle \psi _s (\vec{R}_1,...,\vec{R}_{N_{at}})|\phi _{\sigma}(\vec{R}_{\alpha}) \rangle|^2\delta(\epsilon-\epsilon_s)$$

一般来说，当原子聚集在一起形成一个凝聚系统时，它们的能级就变成了“能带”，我们可以把每个原子看到的能带看作局域态密度所描述的能带，因此我们可以得到：

$$U^{tot}_{TB}=2\sum _{\alpha,\sigma}\int^{+\infty}_{-\infty}\epsilon n(\epsilon)D_{\alpha \sigma}(\epsilon)d\epsilon=2\sum _{\alpha,\sigma}\int^{\epsilon _F}_{-\infty}\epsilon D_{\alpha \sigma}(\epsilon)d\epsilon=\sum _{\alpha}F_{\alpha}$$

其中$n(\epsilon)$表示占据几率，表达式的最后一行非常有用因为在使用经典势时，总能总是写为原子能量的加和，即$E=\sum_{\alpha}E_{\alpha}$。因此，这一关系是我们在量子世界和经典世界之间建立桥梁的关键。

为了精确地获得$D_{\alpha \sigma}(\epsilon)$，原则上需要知道晶体中所有原子的位置，更进一步，$D_{\alpha \sigma}(\epsilon)$是一个关于这些位置的非常复杂的函数，然而，为了达成我们的目的，我们通常不需要计算$D_{\alpha \sigma}(\epsilon)$的详细结构，为了估计这些量如包括$D_{\alpha \sigma}(\epsilon)$积分的$F_{\alpha}$,我们只需要关于它的宽度和形状的大致特征的信息。这一信息可以通过对$D_{\alpha \sigma}(\epsilon)$的积分很容易地获得，定义为：

$$\mu^{\alpha\sigma}_p=\int^{+\infty}_{-\infty}\epsilon ^p D_{\alpha \sigma}(\epsilon)d\epsilon$$

用上式我们可以写作：

$$\mu^{\alpha \sigma}_p=\sum_{\alpha_1 \sigma_1...,\alpha_{p-1}\sigma_{p-1}}\langle \phi_{\sigma}(\vec{R}_{\alpha})|\hat{H}|\phi_{\sigma 1}(\vec{R}_{\alpha 1}) \rangle...\langle \phi_{\sigma _{p-1}}(\vec{R}_{\alpha _{p-1}})|\hat{H}|\phi_{\sigma}(\vec{R}_{\alpha}) \rangle$$

因此p阶矩可以通过紧束缚哈密顿量H的元素的加和来计算，注意$\mu^{\alpha \sigma}_{0}=1$以及$\mu^{\alpha \sigma}_1$代表原子的平均能量，与能量标度的零点选择有关。因此关于$D_{\alpha \sigma}(\epsilon)$形状的真正相关信息包含在$\mu^{\alpha \sigma}_2$和更高阶矩中。

在过渡金属的特殊情况下，人们认为过渡金属的性质以d带的填充情况为特征，并且在许多情况下，我们首先可以近似地忽略掉s电子和p电子。因此归为d轨道的态密度$D_{\alpha \sigma}(\epsilon)$可以分到d轨道态密度$D_{\alpha d}(\epsilon)$。根据这种近似，只保留了d带对应的态密度，为了简单起见，在下面的步骤中我们将忽略轨道量子数，本着与过渡金属相同的精神，我们将假设可以通过只考虑一个能带来表征一种材料。

如果我们假设平均能量为零，那么二阶矩是一个方差，代表了局域态密度的能量宽度或带宽的平方。更高阶矩描述了能带形状，在二阶矩近似下我们可以得到紧束缚近似下的总能为：

$$U^{tot}_{TB}=\sum _{\alpha}F[\mu _2^{\alpha}]=-A\sum_{\alpha}(\mu_2^{\alpha})^{1/2}=-A\sum_{\alpha}\sqrt{\sum_{\beta} H^2_{\alpha \beta}}$$

尝试用从头算方法来计算矩阵元给出的定量结果很差，对于经验拟合，矩阵元素$H^2_{\alpha \beta}$可以被看作是结合势函数，它描述了局域环境并且仅仅取决于原子α和原子β之间的距离。在下文中，与EAM势类似这些函数被写作$\rho(R_{\alpha \beta})$并且被拟合为与从头算或实验数据一致。

为了处理紧束缚成对泛函的问题，有必要通过防止晶格坍塌的斥力来增加电子能带能量$U^{tot}_{TB}$的吸引，这个力的物理基础就是价电子气体压缩产生的泡利斥力，有了这些概念，我们可以把总能量写成：

$$E_{tot}=\frac{1}{2}\sum_{\alpha,\beta}V(R_{\alpha\beta})+\sum_{\alpha}F[\mu^{\alpha}_2]=\frac{1}{2}\sum_{\alpha,\beta}V(R_{\alpha \beta})-A\sum_{\alpha}\sqrt{\sum_{\beta}\rho(R_{\alpha \beta})}$$

紧束缚键模型给出了将$E_{tot}$表示为一对势能项和一个紧束缚电子能带项之和的理由。

在对过渡金属进行压缩或对某些合金进行建模的情形下，s电子和d电子在表征材料方面起着重要的作用，在这些情况下，与d轨道类似，s轨道被分进s带组，在这一方案中，保留了两个带，产生的总能量为：

$$E_{tot}=\frac{1}{2}\sum _{\alpha,\beta}V(R_{\alpha \beta})+\sum_{\alpha}F_s[\mu^{\alpha s}_2]+\sum_{\alpha}F_d[\mu^{\alpha d}_2]$$

这种形式的形状记忆合金在紧束缚模型中被称为双带模型，也可以被用于磁性建模中。

接下来我们将讨论一些在形状记忆合金中常用的紧束缚泛函，这类泛函中第一类是Finnis-Sinclair泛函，对于该泛函，排斥部分$V(R_{\alpha \beta})$和结合部分$\rho(R_{\alpha \beta})$都被设定为短程的，并且被参数化了，来拟合7种bcc过渡金属的晶格常数，结合能和三种弹性模量，对于结合势$\rho(r)$采用抛物线的形式，表达式如下：

$$\rho(r)=(r-d)^2\theta(d-r)$$

而对于成对势V®，采用了四次多项式的形式，表达式为：

$$V(r)=(r-c)^2(c_0+c_1 r+c_2 r^2)\theta(c-r)$$

其中参数c和d是截止半径，被设定为落在第二到第三近邻原子之间，$c_0,c_1,c_2$三个参数和A被用来拟合实验数据，该函数可以解释实验的空位形成能，并且不需要外加压力来平衡"柯西压力"。

Ackland发展了同样类型的函数来描述fcc、bcc和hcp金属，对于fcc和hcp金属，势能采取立方的形式：

$$V(r)=\sum^6_{k=1}a_k(r_k-r)^3\theta(r_k-r),r_1\gt r_2\gt ... \gt r_6$$

$$\rho(r)=\sum^2_{k=1}A_k(R_k-r)^3\theta(R_k-r),R_1\gt R_2$$

其中参数$r_1$和参数$R_1$分别表示V和ρ的截止半径，而所有其它的参数都被用来拟合实验数据，这些数据通常是晶格常数，结合能，弹性常数$C_{11},C_{12},C_{44}$和柯西压力。注意，在这种形式中，全局缩放因子A被忽略了，取而代之的是两个相互独立的缩放因子$A_k$，对于bcc晶格，上述形式被修改为Ackland-Thetford函数形式，表达式为：

$$\rho(r)=\theta(d-r)(r-d)^2$$

$$V_2(r)=\theta(c-r)(r-c)^2(c_0+c_1r+c_2 r^2)+B\theta(b_0-r)(b_0-r)^3e^{-\alpha r}$$

传统上讲，以上Finnis-Sinclair函数通常被用于fcc和bcc金属的模拟，而EAM势已经主要被用于fcc金属，没有特别的理由认为这两种方法更适合何种晶体类型，尽管F为负平方根的限制可能会使Finnis-Sinclair函数的灵活性降低。EAM的二阶矩观点的一个吸引人的方面是，它提供了一条通往更精确势函数的自然途径。通过递归方法或其它方法将能量表达式扩展到包含更高阶矩的项，可以更真实地表示化学键地复杂性。更高阶矩可以由哈密顿量点积产生，哈密顿量点积表示原子间跳跃更多的路径，两种方法的对比如下：

3.TB和EAM势的经验拓展

在文献中，可以找到很多专门针对TB和EAM方法的扩展。在所有情况下，这些扩展都必须增加自由参数的数量来拟合材料的某些额外特性，这些特性在EAM和TB框架中不是兼容的。下面总结了一些成功的改进。

3.1改进的嵌入原子势

改进的嵌入原子势(Modified Embedded Atom Method,MEAM)是在传统的嵌入原子势的基础上的一个经验扩展，最初被设计用于复现所有过渡金属的弹性常数，包括具有负的柯西压力的过渡金属(如Cr)。MEAM背后的想法是包含键角的作用，EAM势没有描述这一作用，因为原子的电荷密度势球对称的，EAM势可以通过两种方式进行修改：

1. 保持EAM势的函数形式不变，并通过角度相关的项来增加球对称原子的电子密度。
2. 保持电子密度不变，但在总能表达式中添加修改后的能量项。

对于第一个选项，总能$E_{tot}$的表达式与前面提到的相同：

$$E_{tot}=\frac{1}{2}\sum_{\alpha,\beta}V(R_{\alpha \beta})+\sum_{\alpha}F[\overline{\rho}_{\alpha}]$$

但是其中平均原子密度$\overline{\rho}_{\alpha}$被修改为：

$$\overline{\rho}_{\alpha}=\rho^{(0)}_{\alpha}+\rho^{(1)}_{\alpha}+\rho^{(2)}_{\alpha}+\rho^{(3)}_{\alpha}$$

在这一表达式中，第一项是球对称的电荷密度(与EAM势的电荷密度相同)，接下来三项是角贡献。不同的角度贡献的显示表达式可以在相关文献中找到。

对于第二个选择，原子的电荷密度保持不变，但是在总能表达式中加入了一个能量修正项，以弥补系统的实际总能与EAM计算得到的总能之间的误差，使用了球对称原子电荷密度的线性叠加：

$$E_{tot}=\frac{1}{2}\sum_{\alpha,\beta}V(R_{\alpha \beta})+\sum_{\alpha}F[\overline{\rho}_{\alpha}]+\sum_{\alpha}M[P_{\alpha}]$$

其中:

$$P_{\alpha}=\sum_{\beta}\rho(R_{\alpha \beta})^2$$

修正项通常被视为指数函数，由下式给出：

$$M[P]=\kappa \left( \frac{P}{P_e}-1 \right)^2exp \left[ -\left( \frac{P}{P_e}-1 \right)^2 \right]$$

其中：

$$\kappa = \frac{n^2F_0}{8}+\frac{9\Omega B-15\Omega G}{8\beta ^2}$$

在这一表达式中，使用了Johnson函数相同的符号(见第2.4节)。常数$P_e$是电荷密度平衡时的修正项参数，常数$G=(3C+2C')/5$是Voigt平均剪切模量，其中$C=C_{44}$,$C'=(C_{11}-C_{12})/2$。

3.2嵌入缺陷法

嵌入缺陷法(Embedded Defect Method,EDM)是对EAM势的扩展，以一种与MEAM相当类似的方式。EDM最初开发的原因与MEAM相同，用于描述过渡金属的弹性常数，尤其是具有负的柯西压力的元素，其对于模拟过渡金属中的缺陷非常有用。

EDM势的形式是为了在EAM势中加入与角度有关的电荷密度。本质上，不是计算每个原子位置的电荷密度，而是计算“偶极电荷密度张量”，如下式：

$$\overline{\overline{\lambda}}_\alpha = \sum_{\beta}\rho(R_{\alpha \beta})(\vec{r}_{\alpha \beta}\otimes \vec{r}_{\alpha \beta})$$

其中$\vec{r}_{\alpha \beta}$是连接原子α和原子β的单位矢量，符号$\otimes$表示张量积，这一张量可分为各向同性的$\overline{\overline{S}}$和所谓的偏张量$\overline{\overline{D}}$(迹为0)，各向同性张量的迹对应于$\overline{\overline{\lambda}}$的不变量，并且不超过EAM平均原子电荷密度$\overline{\rho}$的三分之一。$\overline{\overline{\lambda}}$的第二个不变量是偏张量的范数，它与角度有关，这一范数表达式如下：

$$Y_{\alpha}=\sum_{i,j}D^{ij}_{\alpha}D^{ij}_{\alpha}$$

在这一框架下，势的多体项是由这两个不变量(能量必须是不变量)的两个泛函F和G，第一个只不过是传统的嵌入函数，第二个是附加的非中心相互作用项：

$$E_{tot}=\frac{1}{2}\sum_{\alpha,\beta}V(\vec{R}_{\alpha}, \vec{R}_{\beta})+\sum_{\alpha}F[\overline{\rho}_{\alpha}]+\sum_{\alpha}G[Y_{\alpha}]$$

正如Pasianot提到的，泛函G是通过键角项原点的线性函数，其中$G'\gt 0$，这样EDM可以被看作EAM势相对于多体角项Y的一阶展开。

3.3对紧束缚的Ackland-Mendelev扩展

对TB方法中的SMA作的经验扩展是为了完全描述点缺陷相互作用和压缩数据，Ackland-Mendelev提出的SMA泛函的扩展形式如下：

$$F[\rho]=-A_1\sqrt{\rho}+A_2\rho ^2+A_3\rho^4$$

F的这种形式结合了动能效应，使我们在跳跃和自由电子占主导地位的区域之间平稳地增加ρ。在这个框架下，各向同性压缩用多体项(ρ较大)处理，而短原子-原子距离用对势处理。

4.有效势

TB方法或EAM方法中成对泛函是局部环境参数$\mu^{\alpha}_2$和$\overline{\rho}_{\alpha}$的高度非线性泛函，有效势理论为在局部环境参数的多项式函数中展开此类泛函提供了工具。这样，局部环境参数p阶的多项式函数，就产生了从多体势到p体相互作用的能量展开。例如，该方法可以用于扩展群项中的EAM泛函，在群变分法(CVM)中很有用。

作为一个例子，我们给出了EAM的扩展，它完全类似于TB方案中的SMA泛函，我们将$\rho^{ref}$看作参考环境，即各种局部环境不会发生剧烈变化的特定(可能是假设的)环境，例如电子平衡密度。对于合适的参考环境，我们可以对嵌入函数进行泰勒展开，如下所示：

$$F[\overline{\rho}_{\alpha}]=F[\rho^{ref}]+\frac{\delta F}{\delta \rho}|_{\rho=\rho^{ref}}(\overline{\rho}_{\alpha}-\rho^{ref})+\frac{1}{2}\frac{\delta^2F}{\delta \rho^2}|_{\rho=\rho^{ref}}(\overline{\rho}_{\alpha}-\rho^{ref})^2+....$$

如果只保留线性项，那么总能可以写作：

$$E_{tot}=\tilde{E}_0+\frac{1}{2}\sum_{\alpha,\beta}V^{eff}(\vec{R}_{\alpha},\vec{R}_{\beta};\rho^{ref})$$

在这个表达式中，常数项和有效对势由下式给出：

$$\tilde{E}_0=E_0+\sum_{\alpha}\left( F[\rho^{ref}]-\rho^{ref}\frac{\delta F}{\delta \rho}|_{\rho=\rho^{ref}} \right)$$

$$V^{eff}(\vec{R}_{\alpha},\vec{R}_{\beta};\rho^{ref})=V(R_{\alpha \beta})+2\overline{\rho}_{\alpha}\frac{\delta F}{\delta \rho}|_{\rho=\rho^{ref}}$$

不难看出，上式中保留高阶项将导致能量膨胀过程中多体势聚集，模拟方法可以应用于簇泛函，其中必须使用多维泰勒展开。

5.对合金的扩展

在本节中，我们将把上述理论扩展到多组分系统，对于有序合金或任何具有多种原子类型的系统，方程中EAM能量表达式可以改写为：

$$E_{tot}=\frac{1}{2}\sum_{\alpha,\beta}V_{t_\alpha t_\beta}(R_{\alpha \beta})+\sum_{\alpha}F_{t_\alpha}[\overline{\rho}_{\alpha}]$$

其中：

$$\overline{\rho}_{\alpha}=\sum_{\beta}\rho_{t_\beta}(R_{\alpha \beta})$$

注意，对势现在取决于原子α的种类$t_{\alpha}$和原子β的种类$t_\beta$，而$\overline{\rho}_{\alpha}$求和中的各项取决于近邻原子种类，这是因为在嵌入新原子之前，将一个原子嵌入主系统所产生的能量变化是主系统电荷密度的泛函，因此，主系统$\overline{\rho}_{\alpha}$在位置α处的平均电荷密度与位置α处嵌入的原子类型无关，综上所述，对于原子类型为A和B的二元合金，完整的EAM能量表达式需要定义$V_{AA},V_{AB},V_{BB},\rho_{A}(r),\rho_{B}(r),F_A[\overline{\rho}],F_B[\overline{\rho}]$。最难计算的部分是混合对势$V_{AB}$,它通常被认为是$V_{AA}$和$V_{BB}$之间的某个中间值。

将EAM势应用到二元合金的一个例子是用于Fe-Cu合金的Ludwig-Farkas泛函，对于混合型的成对相互作用势，使用以下形式：

$$V^{eff}_{FeCu}(a+bx)=A[V^{eff}_{Fe}(c+dx)+V^{eff}_{Cu}(e+fx)]$$

其中x取从0到1的值，对参数a、b、c、d、e、f和A进行了调整使得整体能够很好地拟合以下数据：(1)α-Fe基体中Cu空位的结合能；(2)α-Fe基体中一个Cu原子的溶解能；(3)Osetsky和Serra定义的α-Fe基体中两个铜原子之间的结合能。

根据TB方法中的SMA泛函，总能$E_{tot}$可以写作：

$$E_{tot}=\frac{1}{2}\sum_{\alpha,\beta}V_{t_\alpha t_\beta}(R_{\alpha \beta})-\sum_{\alpha}\left( \sum_{\beta}\rho_{t_\alpha t_\beta}(R_{\alpha \beta}) \right) ^{1/2}$$

值得注意的是，EAM和SAM之间在形式上实际只存在细微的形式差异，这是因为它们的物理起源不同。在EAM势中，原子α的密度求和表达式项取决于相邻β原子的类型，而与α原子的类型无关，这是因为β原子上固定的电荷与α原子无关。在相应的SMA表达式中，这些项的含义不同：它们是原子α和原子β之间的矩阵元素的平方。为了构建二元合金势，相较于EAM势，SMA势要求更多的泛函$(\rho_{t_\alpha t_\beta}(r))$。

将TB方法中的SMA泛函应用到二元合金的一个例子是FeCu合金的Ackland-Bacon泛函，混合对势的参数由下式给出：

$$V_{AB}(r)=\sum^6_{k=1}a_k^{AB}\theta(r_k^{AB}-r)(r_k^{AB}-r)^3$$

通过该式可以拟合出每个原子的溶剂热，对于稀溶液，即是单取代杂质(SSI)能。使用铁中的铜和铜中的铁的未弛豫SSI能作为拟合数据，对于交叉项势函数$\rho _{AB}(r)$，使用纯元素势函数的几何平均值：

$$\rho_{AB}(r)=\sqrt{\rho_{AA}(r)\rho_{BB}(r)}$$

6.对称性

对于纯元素的EAM势和TB模型下的SMA泛函，有两种变换使原子的能量保持不变，从而使总能量保持不变。这种变换称为对称性。

对于α处的原子，能量可以写作：

$$E_{\alpha}=\frac{1}{2}\sum_{\beta \neq \alpha}V(R_{\alpha \beta})+F[\overline{\rho}_{\alpha}]$$

其中

$$\overline{\rho}_{\alpha}=\sum_{\beta \neq \alpha}\rho(R_{\alpha \beta})$$

很容易验证以下变换：

$$\begin{cases} \tilde{\rho}(R_{\alpha \beta})=S\rho(R_{\alpha \beta}) \\ \tilde{F}[\overline{\rho}_{\alpha}]=F[\overline{\rho}_{\alpha}/S] \end{cases}$$

并且有：

$$\begin{cases} \tilde{F}[\overline{\rho}_\alpha]=F[\overline{\rho}_{\alpha}]+C\overline{\rho}_{\alpha} \\ \tilde{V}(R_{\alpha \beta})=V(R_{\alpha \beta})-2C\rho(R_{\alpha \beta}) \end{cases}$$

对于常数S和C，原子的位点能$E_{\alpha}$保持不变。需要注意的是这些变换并不适用于合金的能量，由于这些变换在不影响纯元素能量的情况下改变了合金的能量，因此可以在拟合过程中使用它们来改善合金势的品质。

这两种对称性的另一个重要结果势，对势V、嵌入函数F和电荷密度都不是唯一确定的，为了唯一地确定对势、嵌入函数和电荷密度，需要两个规范条件：每个对称性下一个。

规范条件的一个例子是有效规范：

1. 第一个条件是嵌入泛函对平衡电荷密度的导数$\overline{\rho}_{eq}$(即完美晶格的密度)

$$F'[\overline{\rho}_{eq}]=0$$

这一条件可以通过变换$C=-F'[\overline{\rho}_{eq}]$很容易地应用于任意函数形式。

2. 第二个条件是将总的平衡电荷密度$\rho_{eq}$标准化为1：

$$\overline{\rho}_{eq}=1$$

这一条件可以通过变换$S=1/\overline{\rho}_{eq}$很容易地实现。